Stosunek objętości Enio: Wyznacz stosunek objętości kuli do objętości ostrosłupa prawidłowego czworokątnego opisanego na tej kuli, jeśli przekrój ostrosłupa zawierający przekątną podstawy i dwie jego krawędzie boczne jest trójkątem równobocznym.

Mila:

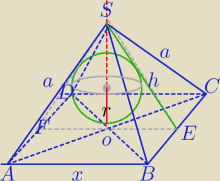
	a√3
|OS|=H=
	2

|AC|=a 1) a²=x²+x² 2x²=a²

	a2
x2=
	2

	1		a3√3
Vo=		*x2*H=
	3		12

2) Promień kuli wpisanej

	1		1		a		a√3
PFES=		x*H=		*		*
	2		2		√2		2

	a2√6
P=
	8

	x+2h
P=		*r
	2

	a√2
W ΔSEC: a2=(		)2+h2
	4

	a√14
h=
	4

	2h+x		a√14+a√2
PFES=		*r=
	2		4

a2√6		a*(√14+√2
	=		*r
8		4

	a*√3*(√7−1)
stąd r=
	6

	4π		a*√3*(√7−1)
3) Vk=		*(		)3}
	3		6

	Vk
4)		=
	Vo

	4π   a*√3*(√7−1)   a*√3*(√7−1)   *( )*( )2 3   6   6
=		=
	a3√3   12

I to już sam dokończ