Oblicz długość promienia okręgu opisanego na trójkącie (trygonometria)? sinus przez cosinus: W trójkącie ABC dane są: |AB| =8, |BC| = C, ∡ ABC = 120^o. Oblicz długość promienia okręgu opisanego na tym trójkącie. Odpowiedź: 2√11 / 3

sinus przez cosinus: PRZEPRASZAM, ODPOWIEDŹ TO 2√111 /3 !

Mila: |BC|= ?

sinus przez cosinus: |BC| = c

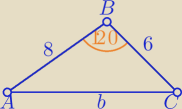
Mila: E tam, |BC|=6 1) tw. cosinusów b²=8²+6²−2*8*6*cos 120^o

	1
b2=64+36−2*48*(−		)
	2

b²=148, b=√4*37=2√37 2) tw. sinusów

b
	=2R
sin120

b=2R*sin120

	√3
2√37=2R*
	2

2√37=R*√3 /*√3 2√111=3R

	2√111
R=
	3

==============