Stereometria Jasiu: Przez krawędź podstawy o długości 10 graniastosłupa prawidłowego trójkątnego o wysokości 17 poprowadzono płaszczyznę nachyloną do podstawy pod kątem α.Wyznacz najmniejszą całkowitą miarę stopniową kąta β takiego, że dla każdego α ∈ (β, 90∘〉 przekrój tego graniastosłupa i rozważanej płaszczyzny jest trapezem. Jak w planimetrii podają długość boku i wysokości, to zawsze trzeba policzyć jakieś magiczne rzeczy :x

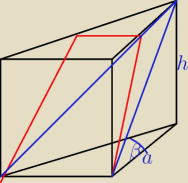
Basia: musi to wyglądać tak jak czerwony trapez kąt nachylenia musi być większy od kąta nachylenia tego niebieskiego trójkąta a = 10 h = 17

	17
tgβ =		= 1,7
	10

β ≈ ..................... odczytaj z tablic α∊(β; 90> dla α=90 przekrojem będzie ściana boczna

Basia: a nie sorry, to ma być kąt nachylenia płaszczyzny przekroju źle przeczytałam

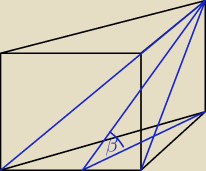
Basia: tu jest ten graniczny kąt β

	H		17		17		17√3
tg β =		=		=		=		≈ ...............
	hp		10√3   2		5√3		15

policz w przybliżeniu i dalej jak poprzednio

Jasiu: Rozumiem już dalszą część zadania, ale nie rozumiem rysunku. Nie wiem, gdzie jest α, ani gdzie ten trapez :s