Geometria w przestrzeni Ewka: Dany jest ostrosłup prawidłowy trójkątny o podstawie ABC i wierzchołku S. Krawędź boczna tworzy z płaszczyzną podstawy kąt 60 stopni. Objętość ostrosłupa jest równa ²₃√3. Oblicz długość krawędzi podstawy tego ostrosłupa.

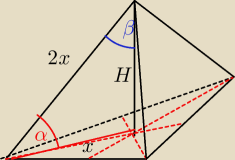
Basia: α=60 ⇒ β=30 H = x√3

	2
x =		hp
	3

	a√3
hp =
	2

	2√3		2√3		a√3		2*3*a		2a
H =		hp =		*		=		=
	3		3		3		3*3		3

bo podstawa jest trójkątem równobocznym

	a2√3
Pp =
	4

	1		a2√3		2a		2a3√3		2√3
V =		*		*		=		=
	3		4		3		36		3

6a³√3 = 72√3 a³ = 12 a = ³√12 sprawdź obliczenia

Eta: a=2 i H=2

Basia: jakiś ułamek jest "do góry nogami" cześć Eto

Eta:

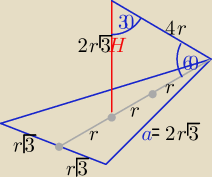
	1
Pp=		*2r√3*3r = 3r2√3 , a=2r√3 i H= 2r√3
	2

	1
V=		*3r2√3*2r√3= 6r3
	3

	2		√3		√3		√3
6r3=		√3 ⇒ r3=		⇒ r3=(		)3 ⇒ r=
	3		9		3		3

	√3
to a= 2r√3= 2*		*√3= 2
	3

a=2

Eta: Hej Basia