zad adam: Na każdej z n>2 planet jest astronom, który obserwuje najbliższą planetę. Zakładając, że n jest liczbą nieparzystą, a odległości między planetami są parami różne, dowieść, że istnieje planeta nieobserwowana.

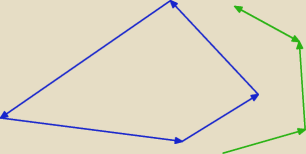
Adamm: załóżmy że planety tworzą figurę zamkniętą (jak na rysunku) jeden astronom może patrzeć tylko na jedną planetę, więc ta figura musi być "skierowana" zgodnie lub przeciwnie ze wskazówkami zegara P₁, P₂, P₃, ..., P_N teraz P₁P₂>P₂P₃>...>P_N−1P_N>P_NP₁>P₁P₂ sprzeczność, więc nie mogą one tworzyć figury zamkniętej w takim razie planety tworzą skierowane "odcinki" jeśli jest taki "odcinek" złożony z 2 planet, to każda patrzy na siebie jeśli z 3 lub więcej, to P₁ patrzy na P₂, ..., P_N−1 patrzy na P_N i P_N musi patrzeć na P_N−1 czyli w takim odcinku na P₁ nikt nie patrzy skoro n jest nieparzyste, to wybierając same odcinki z dwóch planet, nie będziemy mieli ich wszystkich, czyli istnieje odcinek z 3 lub więcej planet, a taki ma planetę "izolowaną"

adam: nie rozumiem