 Proszę o pomoc, bo nie mam na to zadanie pomysłu.
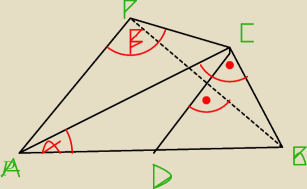
W trójkącie prostokątnym ABC punkt D jest środkiem przeciwprostokątnej AB oraz |∡A|=α. Punkt P
jest obrazem punktu B w symetrii osiowej względem prostej CD oraz |∡APC|=β. Wykaż, że jeśli
α=28 stopni, to β= 118 stopni.
Przepraszam za mój "piękny" rysunek
Proszę o pomoc, bo nie mam na to zadanie pomysłu.
W trójkącie prostokątnym ABC punkt D jest środkiem przeciwprostokątnej AB oraz |∡A|=α. Punkt P
jest obrazem punktu B w symetrii osiowej względem prostej CD oraz |∡APC|=β. Wykaż, że jeśli
α=28 stopni, to β= 118 stopni.
Przepraszam za mój "piękny" rysunek 
 |<APC|=90o+α
dla α= 28o
|<APC|=118o
|<APC|=90o+α
dla α= 28o
|<APC|=118o


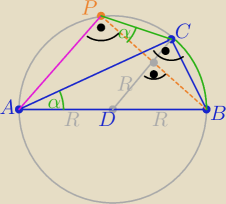
 Punkt P jest końcem cięciwy BP
zatem czworokąt ABCP jest wpisany w okrąg
to |<APC|=180o −|<ABC|= 180o−62o= 118o
Punkt P jest końcem cięciwy BP
zatem czworokąt ABCP jest wpisany w okrąg
to |<APC|=180o −|<ABC|= 180o−62o= 118o