Planimetria Niemądry: Dany jest trójkąt ABC o obwodzie 80. Dwusieczna kąta wewnętrznego A dzieli bok BC na odcinki BD = 8 DC=12. Oblicz długości boków trójkąta. Mam problem z tym zadaniem, ogólnie to nir wiem jak wykorzystać tą dwusieczną. W Tw. Cosinusów mam za dużo niewiadomych. Proszę o wskazówkę

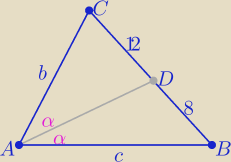
Eta: c+b+20=80 ⇒ c+b=60 z tw. o dwusiecznej:

b		12		3		3
	=		=		⇒ b=		c
c		8		2		2

	3
to c+		c=60 ⇒ 5c=120 ⇒ c=24
	2

to b= 60−24= 36 c=24 , b=36 =========

Niemądry: Oooo, a więc to twierdzenie jest warte zapamiętania. Dziękuję Eta !

Eta: Nie tylko "warte"......... ale ważne !

Niemądry: Pomożesz mi tutaj jeszcze z jednym ?

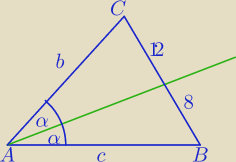
Mila: b+c+8+12=80 1) Z tw. o dwusiecznej kata w Δ:

c		b
	=
8		12

	3
b=		c
	2

3
	c+c=60
2

5
	C=60
2

c=24 b=36 a=20 ====

Niemądry: W skrócie, mamy trójkąt rownoramienny, podstawa wynosi a. Wysokość opuszczona na podstawę to H a na ramię h. Kąt między ramieniem a wysokością H to α. Mam wykazać, że jeśli a² = Hh to sinα = √2 − 1. Obliczyłem, że ramie r = aH / h Więc sinα = U {a/2}{r} = h/2H

Niemądry: Witaj Milu, dziękuję Tobie również

Mila: Z. a² = H*h⇔

	a		h
(*)		=
	H		a

1) W ΔADB:

	h		h
sinβ=		⇔sin(90−α)=		⇔
	a		a

	h
cosα=
	a

2)

	0.5a
W ΔCEB: tgα=		⇔
	H

	a
2tgα=
	H

3) podstawiamy do (*) 2tgα=cosα 2sinα=cos²α 2sinα=1−sin²α sin²α+2sinα−1=0 i sinα>0 Δ=8

	−2−2√2		−2+2√2
sinα=		<0 Lub sinα=
	2		2

sinα=√2−1 =========== Może Eta poda inny sposób

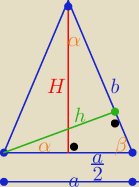
Eta: Z porównania pól a*H=b*h /*h aHh= bh² i z treści zadania a²=Hh

	a		(h
to a3=bh2 ⇒		=		)2
	b		a

sinα= a/2b i cosα=h/a

	1
to sinα=		cos2α ⇒ 2sinα= 1−sin2α
	2

sin²α+2sinα−1=0 , Δ=8 .................... sinα= √2−1 ===========

Eta:

	a		h
Poprawiam zapis ...........		= (		)2
	b		a