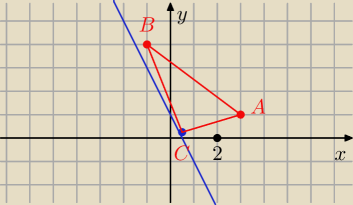
wyliczyłam pr AB y=-3/4+ 3 1/4 co dalej ? :( heelp: Dane sa punkty A = (3, 1) i B = (−1, 4) oraz prosta k o równaniu y = −2x + 1. Wyznacz taki punkt C prostej k, aby suma kwadratów boków trójkata ABC była najmniejsza mozliwa. ˙ Oblicz te najmniejsza sume kwadratów długosci boków.

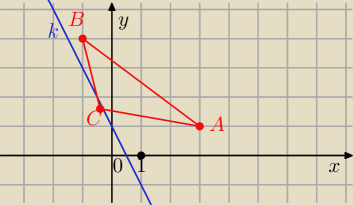
Janek191: A = ( 3, 1) B = ( −1 , 4) C = ( x, −2 x + 1) y = I AB I² + I BC I² + I CA I² = = 4² + 3² + ( x + 1)² + ( −2 x − 3)² + ( 3 − x)² + ( 2 x)² = = 25 + x² + 2 x + 1 + 4 x² +12 x + 9 + 9 − 6 x + x² + 4 x² = = 10 x² − 8 x + 44 f(x) = 10 x² − 8 x + 44

	8		2
x = p =		=
	20		5

wtedy y = f( 0,4) = 10* 0,16 − 8*0,4 + 44 = 1,6 − 3,2 + 44 = 42,4 ==================================================

Janek191: C = ( 0,4 ; 0,2) ============

Janek191: C = ( 0,4 ; 0,2) ============ Sprawdź, czy nie pomyliłem się w rachunkach.

heelp: dzięki a co to za wzor? y = I AB I2 + I BC I2 + I CA I2 co to za wzor ?

Janek191: Suma kwadratów długości boków Δ ABC.

Janek191: Była pomyłka Powinno być: y = 10 x² + 8 x + 44

	− 8
x = p =		= −0,4
	20

y = 10*0,16 − 3,2 + 44 = 42,4 C = ( − 0,4; 1,8) ===============

Janek191: Była pomyłka Powinno być: y = 10 x² + 8 x + 44

	− 8
x = p =		= −0,4
	20

y = 10*0,16 − 3,2 + 44 = 42,4 C = ( − 0,4; 1,8) ===============

Janek191: Była pomyłka Powinno być: y = 10 x² + 8 x + 44

	− 8
x = p =		= −0,4
	20

y = 10*0,16 − 3,2 + 44 = 42,4 C = ( − 0,4; 1,8) ===============

Janek191: Strasznie mi "muli" Internet

heelp: dzieki