geometria analityczna adaśko: Dane są wierzchołki trójkąta ABC: A(2,2) B(9,5) i C(3,9). Z wierzchołka C poprowadzono wysokość tego trójkąta, która przecina bok AB w punkcie D. Wyznacz równanie prostej przechodzącej przez punkt D i równoległej do boku BC. Nie wiem czy dobrze rozumiem ale punkt D jest środkiem odcinka |AB|. Tak więc wyliczylem punkt D i obliczylem równanie prostej |CB|. Później wyznaczylem równanie prostej przechodzącej przez punkt D i podstawiłem do niej współczynnik kierunkowy a prostej |BC|. Czy mógłby ktoś sprawdzić czy obliczenia są dobre? https://iv.pl/images/47902822466482159234.jpg https://iv.pl/images/08597546467726820265.jpg https://iv.pl/images/23317532371093006082.jpg

adaśko: prosze

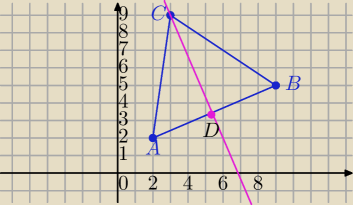
Mila: A(2,2) B(9,5) i C(3,9) 1) prosta AB: 2=2a+b 5=9a+b −−−−−−−−−−−

	3		8
a=		, b=
	7		7

	3		8
y=		x+
	7		7

2) Prosta CD CD⊥AB

	7		7
y=−		x+b i 9=−		*3+b, b=16
	3		3

	7
y=−		x+16
	3

3) D− Punkt przecięcia prostych

3		8		7
	x+		=−		x+16
7		7		3

	156		100
D=(		,		)
	29		29

4) prosta równoległa do BC i przechodząca przez punkt D Teraz spróbuj sam dokończyć.

Krzysiek60:

	4		156		100
y= −		(x−		)+
	6		29		29

dokoncz obliczenia

adaśko: bardziej chodzilo mi na tym czy dobrze zrobilem to zadanie a jesli nie to gdzie jest blad

adaśko: dobrze juz wiem gdzie popelnilem blad, trojkat nie jest rownoramienny