Prawdopodobieństwo - dowód szalony0: Witam, czy mógłby mi ktoś wyjaśnić to zadanie?

	1
|P(A∩B)−P(A)P(B)|≤
	4

Mam zrobić dowód tego, niestety nie mogę za bardzo dojść do tego jak zacząć

szalony0: Czy da się to zrobić jakoś inaczej niż używając Cauchy'ego−Schwarza

Wiercipięta: Proszę o pomoc

Wiercipięta: Też mam to zadanie do zrobienia

PW: Mały kroczek to lepiej niż nic. Przypuśćmy, że (1) A∩B=∅, wówczas B⊂A', a więc P(B)≤P(A')=1−P(A) Nierówność ma postać

	1
|P(A)P(B)|≤
	4

i jest prawdziwa, gdyż po oznaczeniu P(A)=x i P(B)=y

	1
xy≤x(1−x)≤		,
	4

ostatnia nierówność jest równoważna nierówności

	1
−x2+x−		≤0, x∊<0, 1>
	4

	1
−(x−		)2≤0
	2

− prawdziwej dla wszystkich x. A co będzie, gdy założenie (1) nie jest spełnione?

szalony0: Ale ja jestem zielony z matmy Mogę mieć pytanie? Ta ostatnia nierówność jest prawdziwa dla wszystkich x czy wszystkich z przedziału <0,1> ? Nie umiałem tego rozpisać, bo na moje P(A∩B) = P(A)P(B) Rozpisywałem to w ten sposób: |P(A)P(B)+P(A')P(A)P(B)−P(A)P(B)−P(A)P(A')P(B)| = |P(A')P(A)P(B)−P(A)P(A')P(B)| skąd A'∩A∩B to zbiór pusty i to samo z A∩A'∩B Tylko nie wiem co z tą 1/4 i też czy taki zapis jest w ogóle słuszny

PW: Nierówność

	1
−(x−		)2≤0
	2

jest prawdziwa dla wszystkich rzeczywistych x (toż to poziom gimnazjum). Miała być prawdziwa dla x z przedziału <0,1>, bo takie nas interesują, a więc tym lepiej. Jest kategoria zdarzeń, dla których P(A∩B)=P(A)P(B) − tzw. zdarzenia niezależne, ale dla nich teza jest oczywista − lewa strona jest zerem.

szalony0: A jakie to np są przykłady zdarzeń losowych, które pokazują że ta nierówność jest optymalna?

Basia:

	1
np. B=A' i P(B) =
	2

	1		1		1
wtedy masz L = |0 −		*		| =
	2		2		4

więc lepszego ograniczenia nie ma

iteRacj@:

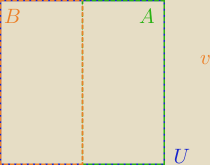
	1		1
P(A)=		, P(B)=		, A∩B=∅, AUB=Ω
	2		2

	1		1		1
wtedy |P(A∩B)−P(A)P(B)|=|0−		*		|=
	2		2		4