Janek191:
x*( x
2 − 5 x + 5) = m
Niech
f(x) = x
3 − 5 x
2 +5 x
więc
f '(x) = 3 x
2 − 10 x + 5 = 0
Δ = 100 − 4*3*5 = 40 = 4*10
√Δ = 2
√10
| | 10 − 2√10 | | 5 | | 1 | |
x1 = |
| = |
| − |
| √10 |
| | 6 | | 3 | | 3 | |
lub
oraz
f ''(x) = 6 x − 10
f ''(x
1} < 0 więc f ma w x
1 maksimum lokalne
f ''(x
2) > 0 więc f ma w x
2 minimum lokalne
y
max = f(x
1)
y
min = f(x
2)
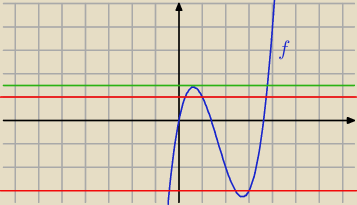
Dla m < y
min lub m > y
max równanie ma 1 rozwiązanie
Dla m = y
min lub m = y
max równanie ma 2 rozwiązania
Dla y
min < m < y
max równanie ma 3 rozwiązania