Planimetria
UczącySię:
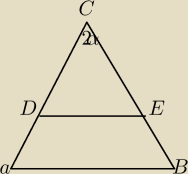
Kąt między ramionami trójkąta równoramiennego ABC ma miarę 2α. Odcinek DE jest równoległy do
podstawy AB. Oblicz długość DE, jeśli AD + BE = ED. Dla jakiej wartości kąta α długość DE jest
równa 2/3 c (c = AB).
(Wybaczcie rysunek)
AD = d, DC = a, EC = b, EB = c...
Więc mam coś takiego:
d+c=EB
| | a | | c | |
sinα = |
| = |
| ⇒ab = dc |
| | d | | b | |
a+d = b+c.
Tutaj się zatrzymałem i nie wiem co zrobić dalej
16 mar 23:36
aniabb: jak równoramienny to po co różne oznaczenia na te same długości boków ?
16 mar 23:41
aniabb:
DE=AB/(1+sinα)
2/3 c=c/(1+sinα)
dla α=30°
16 mar 23:52
UczącySię: Racja, to było głupie. Ale wciąż nie rozumiem jak wyliczyłaś to DE, nie widzę tego.
17 mar 00:03
aniabb:
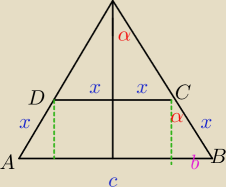
sinα=b/x więc b=xsinα
c=2x+2b=2x+2xsinα=2x(1+sinα)
17 mar 00:12
UczącySię: O kurcze, już wszystko jasne, dzięki wielkie !
17 mar 00:14