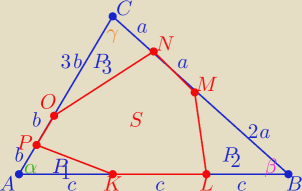
Dowód Słonik: Dany jest trójkąt ABC o polu S. Na boku AB obrano punkty K i L takie, że AK = KL = LB. Na boku BC obrano punkty M i N takie, że BM = 2MN = 2NC. Na boku CA obrano punkty O i P takie, że CO = 3OP = 3PA. Oblicz pole sześciokąta KLMNOP.

Eta:

	1		1		1
P1=		bc*sinα i P=P(ABC)=		3c*5b*sinα ⇒ P1=		P
	2		2		15

	1		1		2
P2=		*c*2a*sinβ i P=P(ABC)=		*3c*5a*sinβ ⇒ P2=		P
	2		2		15

	1		1		3
P3=		*a*3c*sinγ i P=P(ABC)=		*5a*5b*sinγ ⇒ P3=		P
	2		2		25

S=P−(P₁+P₂+P₃)=................. dokończ

Słonik: Dziękuję 😊