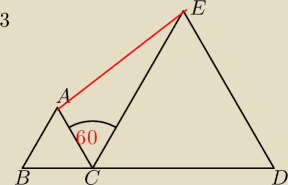
4 zadania Szymon: 1. Wykaż, że 1 : (√1 + √3) + 1 : (√3 + √5) + 1 : (√5 + √7) + 1 : (√7 + √9) jest liczbą naturalną. 2. W trapez równoramienny o ramionach długości 13 cm i krótszej podstawie długości 5 cm wpisano okrąg. Oblicz pole tego trapezu. 3. Na oceanie jest 5 wysepek A, B, C, D, E. Niektóre odległości między nimi są znane, a mianowicie |AB| = |BC| = |AC| = 3 km, |CD| = |DE| = |EC| = 8 km, |BD| = 11km. Oblicz odległość wysepek A i E. 4. Dany jest kwadrat i prostokąt. Jeden z boków prostokąta jest o 3 cm krótszy od boku kwadratu, a drugi bok prostokąta o 4 cm dłuższy od boku tego kwadratu. Jaka powinna być długość boku kwadratu, aby jego pole było większe od pola prostokąta? Podaj wszystkie rozwiązania, jeśli długość boku kwadratu jest liczba naturalna. Z góry dziękuje

Janek191: 1)

1		√3 − 1
	=
√1 + √3		2

1		√5 − √3
	=
√3 + √5		2

1		√7 − √5
	=
√5 + √7		2

1		√9 − √7
	=
√7 + √9		2

Po dodaniu prawych stron otrzymamy

	√3 − 1 + √5 − √3 + √7 − √5 + 3 − √7
w =		= 1
	2

g: 1.

	√3−1		√5−√3		√7−√5		3−√7		3−1
=		+		+		+		=		= 1
	2		2		2		2		2

3. |AE|² = 3² + 8² − 3*8*cos 60 jest też drugie rozwiązanie. jeśli A będzie z drugiej strony odcinka BC to |AE| = 8+3 4. a² > (a−3)*(a+4) = a² + a −12 czyli a < 12, ale a > 3 żeby mógł istnieć prostokąt w sumie a = 4,5,6,7,8,9,10,11

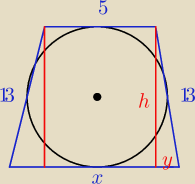
Janek191: Mamy 2*13 = 5 + x 26 = 5 + x x = 21 y = ( 21 − 5) : 2 = 8 więc h² = 13² − 8² = 169 − 64 = 105 h = √105 więc P = U{21 + 5}{2]* √105 = 13√105 ================================= II sposób p = (5 + 2*13 + 21 ) : 2 = 26 zatem p − 5 = 21 p − 13 = 13 p − 13 = 13 p − 21 = 5 P = √ 21*13*13*5 = 13 √105 ===========================