Zadania z Logiki kleszcz: https://ufile.io/iwngx > Link bezpieczny do pobrania zadań. Moje odpowiedzi: Zad 1. a)0(fałszywe) b)1(prawdziwe) c)1(prawdziwe) d)0(fałszywe) Zad 2. a)0(fałszywe) b)0(fałszywe) c)1(prawdziwe) d)0(fałszywe) e)1(prawdziwe) Zad 3. I tutaj mam problem w jaki sposób tworzy się negację bo wyszło mi że w a) będzie 0(fałszywe)?

kleszcz: Nie musi być wszystko na raz, ale to pilne

heheszek: nie ufam takim "bezpiecznym" linkom.

heheszek: albo wstaw zadanie tutaj albo podaj link do strony gdzie sie od razu zdjecie pojawi.

kleszcz: Ifotos zdjęcia: > https://ifotos.pl/z/qnensas > https://ifotos.pl/z/qnensaa > https://ifotos.pl/z/qnensqr > https://ifotos.pl/z/qnensqn Zadanie 4. Treść > Oceń wartość logiczną podanych zdań oraz napisz ich zaprzeczenia.

kleszcz: ?

iteRacj@: widocznie nikt nie ma czasu wpisywać tych przykładów tutaj, a bez tego skutecznie nie wyjaśni się odpowiedzi...

heheszek: zad 1. a) 0 − ok b) 1 − ok c) 1 − ok d) 0 − ok zatem pierwsze masz ok. zad 2. a) 1 − masz blednie (bo kazda liczba pierwsza jest nieparzysta) b) 1 ⇔ 1 −−> wynik to 1 (masz blednie) c) 1 ⋀ 1 −−> wynik to 1 (ok) d) 0 (ok) e) 1 (ok)

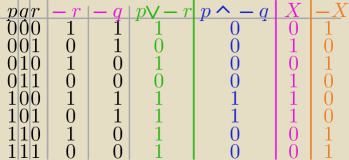
xyz: 3. X − nie zmieścił mi napis wiec wrzuciłem X oczywiście pod tym iksem kryje się: (p ⋁ ~ r) ⇒ (p ⋀ ~ q) natomiast − X oznacza negacje tego co wyżej czyli: ~ [(p ⋁ ~ r) ⇒ (p ⋀ ~ q)] i jak masz te tabelkę to szukasz jakiegoś powiązania

heheszek: zad, 3 skorzystaj z praw de morgana i innych takich jak np. co robi negacja implikacji przykladowo a) napisac negacje: (p ⋁ ~ r) ⇒ (p ⋀ ~ q) wiec co robimy? negujemy podwojnie zeby nie zmienic wartosci wyrazenia bo negacja negacji daje wyrazenie bez zmian zatem ~[~[(p ⋁ ~ r) ⇒ (p ⋀ ~ q)]] i teraz negacja implikacji ∼(a⇒b) jest rownowazna a ⋀ (∼b). zatem ~[(p ⋁ ~ r) ⋀ ~(p ⋀ ~ q)]] negacja iloczynu (z praw de morgana) to suma negacji ~(a ⋀ b) to (~a ⋁ ~b), wiec mamy negacje iloczynu gdzie tym 'a' jest (p ⋁ ~ r) , natomiast 'b' to (~p ⋁ q) a wiec to ~[(p ⋁ ~ r) ⋀ ~(p ⋀ ~ q)]] jest rownowazne [~(p ⋁ ~ r) ⋁ (p ⋀ ~ q)]] no i na koniec negacja sumy [kolejne prawo de morgana] ktore mowi, ze: ~ (a V b) to to samo co (~a ⋀ ~b) (~p ⋀ r) ⋁ (p ⋀ ~ q) i to jest nasz wynik mozna zrobic tabelke prawdy i sprawdzic czy sie zgadza.

UczącySię: heheszek a liczba 2 ? Jest parzysta i pierwsza

heheszek: hehe faktycznie, zapomnialem o tej nieszczesnej dwojce. tam powinien byc falsz

kleszcz: No właśnie mam dobrze, gdyż liczba 2 to liczba pierwsza

kleszcz: A w b) mamy 3>bądź równe 0 czy 3 jest równe 0 no raczej nie xD więc mamy równoważność 1 > 0 to 0(zdanie fałszywe).

kleszcz: Chyba że to źle interpretuje...(?)

heheszek: Jak dla Ciebie 3 ≥ 0 jest falszywe to co Ty na matematyce w gimnazjum miales o szkole srednia nawet nie pytam

kleszcz: Czy 3 jest większe LUB RÓWNE 0 Czy 3=0?

kleszcz: 3 NIE RÓWNE 0

kleszcz: Jeśli mamy 3>0 wtedy jest prawdziwe 3 ≥ 0 − fałszywe.

kleszcz: Ale negacji wciąż nie ogarniam, muszę chyba kupić kurs Matematyka Dyskretna Krystian Karcz. Ktoś może ma ten kurs?

123: Jest chyba pewna różnica między większe równe, a po prostu równe...

kleszcz: OK 123 w sumie racja ale w takim razie dlaczego ma być to zdanie prawdziwe w takim razie?

iteRacj@: sprawdź w notatkach albo w internecie, kiedy prawdziwa jest alternatywa i kiedy prawdziwa jest równoważność

kleszcz: OK racja sorka w b) miałem źle

kleszcz: Czy w zadaniu 5 z tautologiami mam przyjąć wartości np: p,q jako 1?

kleszcz: OK ktoś sprawdzi zadanie 5) mam tak że wszystkie zdania są tautologiami(zakładając że są to zdania o wartości logicznej 1) oprócz ostatniego przykładu h) który wychodzi wartość logiczna 0, czyli zdanie nie jest tautologią. Dobrze mam to ostatnie?

kleszcz: Tautologie?

kleszcz: :(

iteRacj@: zdanie złożone h) nie jest tautologią sprawdziłam tylko to jedno

kleszcz: OK dzięki

kleszcz: https://ifotos.pl/z/qnesenw > Dobrze mam to 3 a)?

kleszcz: https://ibb.co/hyg35H > Jak nie działa zdjęcie to tutaj zadziała.

kleszcz: ?

kleszcz: Hallo?

kleszcz: Dobrze policzylem ktos zobaczy?

kleszcz: :(?

aniabb: tabelka dobrze..a o co chodzi w całości to ciężko się domyśleć

kleszcz: Miałem wykonać negację(zaprzeczenie) tego zdania co w przykładzie a)

aniabb: no to negacją (p ⋁ ~ r) ⇒ (p ⋀ ~ q) jest (p ⋁ ~ r) ⋀ (~p ⋁ q) i koniec

aniabb: i ewentualnie tabelka z postu z 16 mar 2018 23:11 (to kolorowe co namalował xyz)

kleszcz: Ale wait negacja implikacji to jak patrzyłem coś równoważność czegoś . Chyba że czegoś nie rozumiem...

kleszcz: https://www.matemaks.pl/prawo-negacji-implikacji.html > powołuje się na jakieś tam źródło xD

kleszcz: Czyli jeszcze trzeba napisać ten znak równoważności chyba.

kleszcz: Aha już wiem tutaj nie trzeba pisać wartości logicznej tylko zwyczajnie napisać jak ona wygląda o to chodzi tak?

aniabb: nie trzeba ..to jest po prostu regułka jakby wzór ... równoważność to tylko że można to podstawić.. tak jak we wzorach znak =

kleszcz: (∼(p→q))⇔(p⋀(∼q)) w takim razie wystarczy taka odpowiedź z tego co rozumiem.

aniabb: tak .. chodzi o to by napisać jak wygląda

aniabb: w 3a możesz napisać ~ [ (p ⋁ ~ r) ⇒ (p ⋀ ~ q) ] <=> [ (p ⋁ ~ r) ⋀ (~p ⋁ q ) ]

kleszcz: Aka OK rozumiem już ale dlaczego się zmieniło z koniunkcji na alternatywę?

aniabb: prawa deMorgana albo skorzystaj z opisu heheheszka z 16 mar 2018 23:25 tylko on niepotrzebnie wstawił jedną negację za dużo bo ty chcesz negację a nie to samo

kleszcz: Że zaprzeczeniem koniunkcji jest alternatywa?

aniabb: tak

kleszcz: Aha dziękuję wreszcie rozumiem

kleszcz: https://ibb.co/d4zXjc > Idę za ciosem i poproszę o sprawdzenie tylko podpunktu b).

aniabb: tak OK

kleszcz: http://ibb.co/fRds2x > Poproszę tylko o sprawdzenie podpunkt c).

aniabb: dużego nawiasu w pierwszej linijce brakuje że negujesz całość

aniabb: i pisz te dodatkowe p q (te w dół) może jakąś inną czcionką bo nieco są mylące...chociaż domyślam się po co one

kleszcz: http://ibb.co/m3nBec > podpunkt d)

kleszcz: a z tym p i q zaraz zmienię bo już zacząłem tak robić

aniabb: w pierwszej linijce negacja przed nawiasem powinna być

kleszcz: http://ibb.co/nRbCKc > podpunkt e)

aniabb: ok

kleszcz: http://ibb.co/jaKrec > ostatni podpunkt f)

kleszcz: Poproszę jeszcze o sprawdzenie.

kleszcz: ?

annabb: Ok

annabb: Chociaż myślę że te mógłbyś poskracac tak jak pisał heheheszek z podwójną negacją

kleszcz: http://ibb.co/gLzOAH > zadadanie 4 podpunkt a) czy odpowiedź na zadanie to wartość logiczna zaprzeczenia tej alternatywy czy wystarczy samo napisanie (1 ⋀ 1) ?

kleszcz: *zadanie

kleszcz: http://ibb.co/csk5qH > Podpunkt b)

kleszcz: http://ibb.co/dwUvPc > Podpunkt c).

kleszcz: http://ibb.co/i5Tsnx > Podpunkt d).

kleszcz: http://ibb.co/bP6Ouc > Podpunkt e).

kleszcz: http://ibb.co/bQjOSx > Podpunkt f).

kleszcz: http://ibb.co/gekBfH > Podpunkt g).

kleszcz: h) Istnieje na świecie żmija, która ma 13 nóg > czy to jest kwantyfikator ∃ i jak zrobić zaprzeczenie(?)

kleszcz: tego kwantyfikatora

ite: Zgodnie z prawem de Morgana mamy: zaprzeczeniem zdania z kwantyfikatorem szczegółowym jest ¬∃_x (p(x)) ⇔ ∀_x(¬(p(x)) ¬∃_żmija (żmija ma 13 nóg) ⇔ ∀_żmija¬ (żmija ma 13 nóg) spróbuj przetłumaczyć na jęz.polski