Rysowanie
Maciess: f(x) = log 12 |x+1|
Określ dziedzine i narysuj wykres funkcji
Df: x∊R\{−1}
Najpierw rysuje log 12 x
Przesuwam o wektor [−1,0]
Wykonuje przekształcenie y=f(|x|)
Dobrze?
16 mar 13:56
Jerzy:

16 mar 14:00
Maciess: Przy ostatnim kroku nie obijam względem osi Y tylko względem asymptoty pionowej x=−1, tak?
Ta asymptota staje się jakby nową osią Y, tak?
16 mar 14:14
Jerzy:
Tak.
16 mar 14:17
Maciess: f(x)= log 12 (|x|+1)
Df: x∊R
log 12 (x)
Przekształcam y=f(|x|)
Przesuwam o wektor [−1,0]
Tak?
16 mar 15:04
Mila:
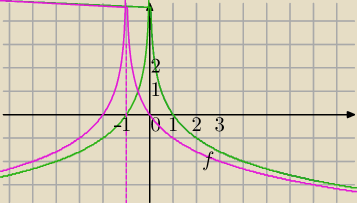
1)
f(x)=log
12(|x+1|)
1)
y=ln
1/2(x)→S
OY tej części wykresu z prawej strony OY⇒
y=ln1/2(|x|)→T
[−1,0]⇒
f(x)=log1/2(|x+1|)
16 mar 18:06
Mila:
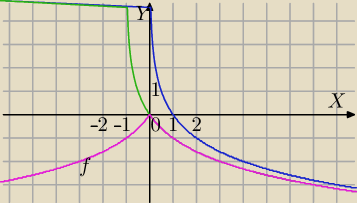
2)
f(x)= log
1/2(|x|+1)
1)
y=log1/2(x) →T
[−1,0]⇒
2)
y=log1/2(x+1) →S
OY tej części z prawej⇒
3)
f(x)= log 1/2(|x|+1)
16 mar 18:13
Mila:
Wykresy trochę "zepsute'' ( u góry odbicie, to wina edytora)
16 mar 18:14
Maciess: Wyszło tak samo tylko miałem problem kiedy odbijam względem OY a kiedy względem tej "nowej OY"
Dziękuje za sprawdzenie Milu

16 mar 18:19
Mila:

16 mar 18:22

 1)
f(x)=log12(|x+1|)
1)
y=ln1/2(x)→SOY tej części wykresu z prawej strony OY⇒
y=ln1/2(|x|)→T[−1,0]⇒
f(x)=log1/2(|x+1|)
1)
f(x)=log12(|x+1|)
1)
y=ln1/2(x)→SOY tej części wykresu z prawej strony OY⇒
y=ln1/2(|x|)→T[−1,0]⇒
f(x)=log1/2(|x+1|)
 2)
f(x)= log 1/2(|x|+1)
1) y=log1/2(x) →T[−1,0]⇒
2)y=log1/2(x+1) →SOY tej części z prawej⇒
3)
f(x)= log 1/2(|x|+1)
2)
f(x)= log 1/2(|x|+1)
1) y=log1/2(x) →T[−1,0]⇒
2)y=log1/2(x+1) →SOY tej części z prawej⇒
3)
f(x)= log 1/2(|x|+1)

