Kula Patrycja123: Z punktu leżącego na powierzchni kuli o promieniu R poprowadzono trzy cięciwy równej długości, tworzące parami kąty o mierze a. Oblicz długości tych cięciw.

Marek: strasznie ciekawe

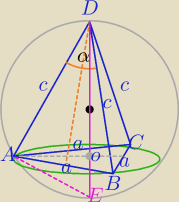
Mila: ABCD− ostrosłup prawidłowy trójkątny. ΔABC−Δrównoboczny

	α		0.5a
1) sin		=
	2		c

	α
a=2c*sin
	2

	2		a√3		a√3		α   2c*√3sin   2
|AO|=		*		=		=
	3		2		3		3

2)ΔEAD− Δprostokątny

c		DE
	=
|OD|		c

c²=2R*|OD|

	α   4c2sin2   2
|OD|2=c2−|AO|2=c2−
	3

	α
|OD|2=c2*(1−(4/3)sin2		)
	2

|OD|=c*(√1−4/3sin²(α/2) 3) c²=2R*c*(√1−4/3sin²(α/2) /:c c=2R*(√1−4/3sin²(α/2) ==================

Patrycja123: na jakiej podstawie wywnioskowałes ze trojkat EAD jest prostokatny

Janek191: Kąt wpisany w koło oparty na średnicy.

Patrycja123: faktycznie, dzieki