Okręgi
Ewelina 500: Dane są dwa zewnętrznie styczne okręgi o promieniach a i b ( a ≠ b) oraz wspólna ich styczna
zewnętrzna.
Niech C będzie punktem styczności tych okręgów, zaś A i B punktami styczności prostej stycznej
i okręgów.
Oblicz promień okręgu wpisanego w krzywoliniowy trójkąt ABC.
Podaj opis konstrukcji szukanego promienia przy zadanych promieniach a i b.
16 mar 11:44
Janek191:
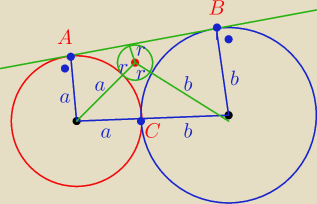
16 mar 12:01
Marek: a jak mam wyliczyc promien

?
16 mar 22:47
aniabb: tak około 3x tw.Pitagorasa

17 mar 00:30
Eta:
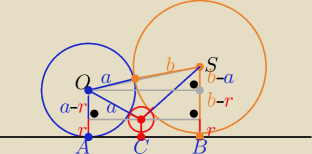
1/ |AB|
2=(a+b)
2−(b−a)
2 = 4ab
2/ |AC|
2=(a+r)
2−(a−r)
2 =4ar
3/ |CB|
2= ((b+r)
2−((b−r)
2 =4br
|AB|= |AC|+|BC|
2
√ab=2
√ar+2
√br
√ab=
√ar+
√br /
2
ab= ar+br +2r
√ab
ab= r(
√a+
√b)
2
17 mar 01:52
aniabb: Ettuś

bo jakoś weny nie miałam do malowania pisanek
17 mar 02:17

 ?
?

 1/ |AB|2=(a+b)2−(b−a)2 = 4ab
2/ |AC|2=(a+r)2−(a−r)2 =4ar
3/ |CB|2= ((b+r)2−((b−r)2 =4br
|AB|= |AC|+|BC|
2√ab=2√ar+2√br
√ab=√ar+√br /2
ab= ar+br +2r√ab
ab= r(√a+√b)2
1/ |AB|2=(a+b)2−(b−a)2 = 4ab
2/ |AC|2=(a+r)2−(a−r)2 =4ar
3/ |CB|2= ((b+r)2−((b−r)2 =4br
|AB|= |AC|+|BC|
2√ab=2√ar+2√br
√ab=√ar+√br /2
ab= ar+br +2r√ab
ab= r(√a+√b)2
 bo jakoś weny nie miałam do malowania pisanek
bo jakoś weny nie miałam do malowania pisanek