Trójkąt Romek000: Wykaż, że jeżeli suma wysokości trójkąta jest 9 razy większa od promienia okręgu wpisanego, to trójkąt ten jest równoboczny

Kasienka: moze na pole podstawiajac wyjdzie

Adamm:

	1		1		1
ha+hb+hc=2*P*(		+		+		)
	a		b		c

	2P
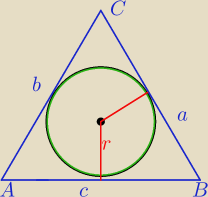
r=
	a+b+c

3		1   1   1   + + a   b   c
	≤		(harmoniczna≤arytmetyczna)
a+b+c		3

równość wtedy i tylko wtedy gdy 1/a=1/b=1/c czyli innymi słowy a=b=c, trójkąt jest równoboczny

Mila: 1) h_a+h_b+h_c=9r

	a+b+c		2P
2) PΔ=P=		*r⇔r=		⇔
	2		a+b+c

	18P
9r=
	a+b+c

	18P
3)		=ha+hb+hc
	a+b+c

a*h_a=b*h_b=c*h_c =2P z równości pól 4)

2P		2P		2P		18P
	+		+		=		⇔
a		b		c		a+b+c

1		1		1		9
	+		+		=
a		b		c		a+b+c

	1		1		1
(		+		+		)*(a+b+c)=9⇔
	a		b		c

b

a

α

c

b

c

(*) 3+(

+

)+(

+

)+(

+

=9

a

b

c

a

c

b

Ponieważ dla dla dodatnich a, b, c wyrażenia w nawiasach są ≥2 i równość zachodzi odpowiednio:

	b		a
(		+		)=2 dla a=b
	a		b

i

	α		c
(		+		)=2 dla a=c i
	c		a

	b		c
(		+		=2 dla b=2 to równość (*) zachodzi dla a=b=c⇔
	c		b

trójkąt jest równoboczny