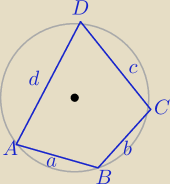
Czworokąt Kinga98: Długość boków czworokąta, w którym można wpisać koło i na którym można opisać koło są równe a,b,c,d. Udowodnij, że pole S tego czworokąta wyraża się wzorem S= √abcd.

Pablo: wykorzystaj to że jeżeli mozna wpisać okrag czyli naprzeciwległe boki a wlasciwie ich suma jest rowna druiej parze bokow naprzeciewległych

Pablo: dalejj, hmmm

Mila: 1) a+c=b+d z warunku, że w czworokąt można wpisać okrąg 2)

	a+b+c+d
PABCD=√(p−a)*(p−b)*(p−c)*(p−d), gdzie p=
	2

z warunku, że na czworokacie można opisać okrąg z (1) p=a+c=b+d P_ABCD=√(a+c−a)*(a+c−b)*(a+c−c)*(a+c−d)= =√c*(a+c−b)*a*(a+c−d)=√c*a*(b+d−b)*(b+d−d)=√a*b*c*d

Kasienka: jest chyba taki wzór jezeli jest okrag opsiany na czworokacie ale nie wiem czy mozna to sposobem wyprowadzajac?