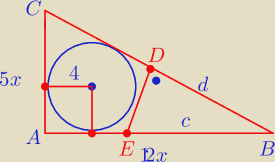
 c2 = (5 x)2 + (12 x)2 = 169 x2
c = 13 x
PΔ = 0,5 r*( 5 x + 12 x + 13 x)
0,5*12 x*5 x = 2*30 x
30 x2 = 60 x
x = 2
więc
AB = 24 , AC = 10, BC = 26
PΔ = 0,5*24*10 = 120 j2
P1 = PAEDC
P2 = PEBD
Mamy
P1 + P2 = 120
c2 = (5 x)2 + (12 x)2 = 169 x2
c = 13 x
PΔ = 0,5 r*( 5 x + 12 x + 13 x)
0,5*12 x*5 x = 2*30 x
30 x2 = 60 x
x = 2
więc
AB = 24 , AC = 10, BC = 26
PΔ = 0,5*24*10 = 120 j2
P1 = PAEDC
P2 = PEBD
Mamy
P1 + P2 = 120
| P1 | 3 | ||
= | ⇒ P1 = 1,5 P2 | ||
| P2 | 2 |
| 120 | 5 | |||
k2 = | = 2,5 = | |||
| 48 | 2 |
 c2 = (5 x)2 + (12 x)2 = 169 x2
c = 13 x
PΔ = 0,5 r*( 5 x + 12 x + 13 x)
0,5*12 x*5 x = 2*30 x
30 x2 = 60 x
x = 2
więc
AB = 24 , AC = 10, BC = 26
PΔ = 0,5*24*10 = 120 j2
P1 = PAEDC
P2 = PEBD
Mamy
P1 + P2 = 120
c2 = (5 x)2 + (12 x)2 = 169 x2
c = 13 x
PΔ = 0,5 r*( 5 x + 12 x + 13 x)
0,5*12 x*5 x = 2*30 x
30 x2 = 60 x
x = 2
więc
AB = 24 , AC = 10, BC = 26
PΔ = 0,5*24*10 = 120 j2
P1 = PAEDC
P2 = PEBD
Mamy
P1 + P2 = 120
| P1 | 3 | ||
= | ⇒ P1 = 1,5 P2 | ||
| P2 | 2 |
| 120 | 5 | |||
k2 = | = 2,5 = | |||
| 48 | 2 |
 c2 = (5 x)2 + (12 x)2 = 169 x2
c = 13 x
PΔ = 0,5 r*( 5 x + 12 x + 13 x)
0,5*12 x*5 x = 2*30 x
30 x2 = 60 x
x = 2
więc
AB = 24 , AC = 10, BC = 26
PΔ = 0,5*24*10 = 120 j2
P1 = PAEDC
P2 = PEBD
Mamy
P1 + P2 = 120
c2 = (5 x)2 + (12 x)2 = 169 x2
c = 13 x
PΔ = 0,5 r*( 5 x + 12 x + 13 x)
0,5*12 x*5 x = 2*30 x
30 x2 = 60 x
x = 2
więc
AB = 24 , AC = 10, BC = 26
PΔ = 0,5*24*10 = 120 j2
P1 = PAEDC
P2 = PEBD
Mamy
P1 + P2 = 120
| P1 | 3 | ||
= | ⇒ P1 = 1,5 P2 | ||
| P2 | 2 |
| 120 | 5 | |||
k2 = | = 2,5 = | |||
| 48 | 2 |
 c2 = (5 x)2 + (12 x)2 = 169 x2
c = 13 x
PΔ = 0,5 r*( 5 x + 12 x + 13 x)
0,5*12 x*5 x = 2*30 x
30 x2 = 60 x
x = 2
więc
AB = 24 , AC = 10, BC = 26
PΔ = 0,5*24*10 = 120 j2
P1 = PAEDC
P2 = PEBD
Mamy
P1 + P2 = 120
c2 = (5 x)2 + (12 x)2 = 169 x2
c = 13 x
PΔ = 0,5 r*( 5 x + 12 x + 13 x)
0,5*12 x*5 x = 2*30 x
30 x2 = 60 x
x = 2
więc
AB = 24 , AC = 10, BC = 26
PΔ = 0,5*24*10 = 120 j2
P1 = PAEDC
P2 = PEBD
Mamy
P1 + P2 = 120
| P1 | 3 | ||
= | ⇒ P1 = 1,5 P2 | ||
| P2 | 2 |
| 120 | 5 | |||
k2 = | = 2,5 = | |||
| 48 | 2 |
 !
!