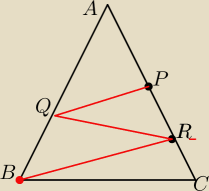
Trojkat rownoramienny Krzysiek60: Trojkat rownoramienny ABC w ktorym AB= AC ma nastepujaca wlasnosc : na ramieniu AC mozemy znalezc takie punkty P i R a na ramieniu AB taki punkt Q ze BC= BR = RQ= QP= PA Oblicz miary kątow trojkata ABC

Krzysiek60: Na razie jedyne co widze to ze ΔCBR=ΔRQP=ΔPQA i wszystkie te trojkaty sa rownoramienne

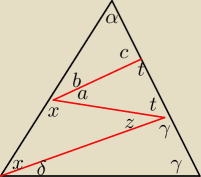
Basia: δ=180−2γ x = γ−δ = 3γ−180 z = 180−2x = 180−6γ+360 = 540 − 6γ t = 180−z−γ = 180−540+6γ−y = 5γ−360 a=180−2t = 180−5y+360 = 540 − 5γ b = 180−a−x = 180−540+5γ−3γ+180 = 2γ−180 jeżeli się nie pomyliłam w rachunkach to to jest niemożliwe bo α=180−2γ c = 180−b−α = 180−2γ+180−180+2γ = 180 ale sprawdzaj

Krzysiek60: Oczywiscie bede sprawdzal Basiu odpowiedz to 80^o, 80^o,20^oC

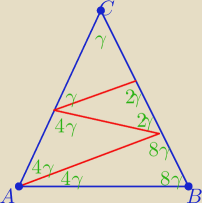
Eta: 17γ= 180^o

	180
<C=γ=		o
	17

	1440
<A=<B=8γ= (		)o
	17

Basia: no to musiałam się pomylić, ale idea chyba musi być taka jak mniej więcej opisałam

Krzysiek60: Dzieki Eta

Eta: Krzysiek ... ale to jest źle ( pomyliłam się jeszcze raz rysuję

Krzysiek60: ja sie domyslilem

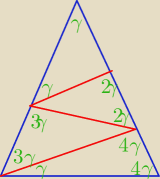
Eta: 9γ=180^o γ=20^o 4γ= 80^o teraz jest ok

Krzysiek60: dziekuje

Krzysiek60: Eta dopki jestes jeszce na forum to wroce do tego zadania jeszcze bo To γγ, 2γ, 2γ 3γ 3γ i 4γ 4γ to byla tylko kolejnosc ? Bo nawet gdyby w tym nawyzym trojkacie gdzie ejst γ i γ potem jest 2γ (kat zewnwtrzny ale potm nie pasuje

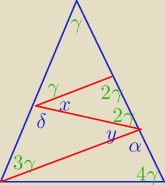
Eta: x= 180^o−4γ γ+δ+x=180^o ⇒ δ= 3γ i podobnie y=180^o−6γ 2γ+y+α=180^o ⇒ α= 4γ

Krzysiek60: Wolalem dopytac .

Eta: