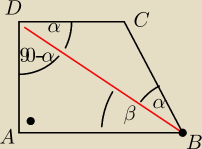
 W czworokacie ABCD kąty przy wierzcholkach A i D sa proste I BC= CD
Wykaz z ew prostej BD zawarta jest dwusieczna kąta B
ΔDBC jest Δrownoramiennym
Wobec tego ∡CDB=∡CBD=α
ΔADB jest trojkatem prostokatnym wiec ∡ADB= 90o−α i ∡ABD= β
nalezy wykazac ze ∡α= ∡β
90−α+β= 90o
stad α=β
Prosta BD jest zawarta w dwusiecznej kąta B
W czworokacie ABCD kąty przy wierzcholkach A i D sa proste I BC= CD
Wykaz z ew prostej BD zawarta jest dwusieczna kąta B
ΔDBC jest Δrownoramiennym
Wobec tego ∡CDB=∡CBD=α
ΔADB jest trojkatem prostokatnym wiec ∡ADB= 90o−α i ∡ABD= β
nalezy wykazac ze ∡α= ∡β
90−α+β= 90o
stad α=β
Prosta BD jest zawarta w dwusiecznej kąta B
 Dzień dobry wieczór
Dzień dobry wieczór 
