 Bardzo, bardzo proszę o pomoc
Bardzo, bardzo proszę o pomoc
 1/
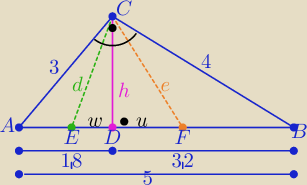
1)rysunek
1/
1)rysunek
| 3*4 | ||
2/ |AB|=................ i h= | =............... | |
| |AB| |
| 2,4 | w | 2,4 | u | ||||
= | = | ||||||
| 3 | 1,8−w | 4 | 3,2−u |
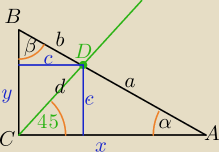 |AC|=x, |BC|=y
1) d=c*√2
|AC|=x, |BC|=y
1) d=c*√2
| 1 | 1 | 1 | ||||
2) | x*y=c2+ | *c*(x−c)+ | (y−c)*c | |||
| 2 | 2 | 2 |
| 1 | 1 | 1 | 1 | 1 | |||||
x*y=c2+ | cx− | c2+ | yc− | c2 | |||||
| 2 | 2 | 2 | 2 | 2 |
| x*y | ||
c= | ||
| x+y |
| x*y√2 | ||
d= | ||
| x+y |
| y | b | xb | |||
= | z tw. o dwusiecznej kąta w Δ⇔y= | ||||
| x | a | a |
| x2*b2 | ||
x2+ | =(a+b)2 | |
| a2 |
| b2 | a2+b2 | |||
x2*(1+ | )=(a+b)2⇔x2* | =(a+b)2 | ||
| a2 | a2 |
| a2 | ||
x2=(a+b)2* | ||
| a2+b2 |
| a*(a+b) | ||
x= | ||
| √a2+b2 |
| b*(a+b) | ||
y= | ||
| √a2+b2 |
| x*y√2 | ||
d= | ||
| x+y |
| ab*(a+b)2 | ||
x*y= | ||
| a2+b2 |
| a*(a+b)+b*(a+b) | (a+b)2 | |||
x+y= | = | |||
| √a2+b2 | √a2+b2 |
| ab*(a+b)2 | √a2+b2 | |||
d=√2* | * | |||
| a2+b2 | (a+b)2 |
| ab√2 | ||
d= | ||
| √a2+b2 |


 Mój mi się nie bardzo podoba, bo "okrężny".
Czy wynik masz taki sam?
Mój mi się nie bardzo podoba, bo "okrężny".
Czy wynik masz taki sam?
| 2xy | ||
P(ABC)= | ||
| 4 |
| xd√2 | y*d√2 | |||
P(ADC)= | P(BDC)= | |||
| 4 | 4 |
| √2xy | ||
to d= | ||
| x+y |
| x | a | a | |||
= | ⇒ x= | y | |||
| y | b | b |
| b(a+b) | a(a+b) | |||
x2+y2=(a+b)2 ⇒ y= | to x= | |||
| √a2+b2 | √a2+b2 |
| (a+b)2 | ||
x+y= | ||
| √a2+b2 |
| √2ab | ||
d= | ||
| √a2+b2 |

