Geometria analityczna
Nel: Przez punkt A(2,1) poprowadź prosta tak, by punkt A był środkiem odcinka tej prostej zawartego
między prostymi 2x+y=0, x−y−2=0.
Podaj równanie szukanej prostej oraz współrzędne końców otrzymanego odcinka.
15 mar 20:01
Janek191:
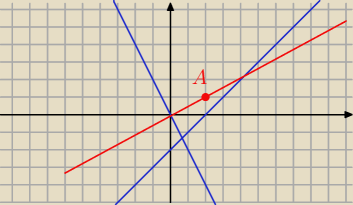
15 mar 20:08
Nel: Ooo dzięki

a mógłbyś napisać też wykorzystales wzory tych prostych?
15 mar 20:11
Janek191:
y = − 2 x
B = ( x, −2 x) A = ( 2, 1)
→
BA = [ 2 − x1, 1 +2 x1 ]
oraz
y = x − 2
C = ( x2, x2 − 2)
→
AC = [ x2 − 2, x2 − 2 − 1] = [ x2 − 2, x2 − 3]
→ →
BA = AC
2 − x1 = x2 − 2 i 1 + 2x1 = x2 − 3
x1 + x2 = 4 i 2 x1 − x2 = − 4
x2 = 4 − x1
2 x1 = 4 − x1 − 4
3 x1 = 0
x1 = 0
y1 = −2*0 = 0
B = ( 0, 0)
========
x2 = 12 x1 + 4 = 4
y2 = x2 − 2 = 2
C = ( 4, 2)
========
15 mar 20:21

 a mógłbyś napisać też wykorzystales wzory tych prostych?
a mógłbyś napisać też wykorzystales wzory tych prostych?