Wyznacz dziedzinę/zbiór wartości funk. tryg. Michał: Hej, raz jeszcze =) Tym razem dwa pytania 1. Jak wyznaczyć dziedzinę tego cudeńka:

	1
f(x)=
	1−tg x

2. Czy dobrze myślę jeżeli idzie o zbiór wartości tej funkcji:

	1
f(x)=
	2+|sin x|

|sin x| ma f(D)= <0;1> to wartość minimalna to 0 max to 1 czyli podstawię do wzoru i wyliczę

	1		1
f(x)=		=
	2+0		2

	1		1
f(x)=		=
	2+1		3

	1		1
f(D)= <		;		>
	3		2

Odpowiedź jest dobra, ale czy tok rozumowania także?

Janek191: 1)

	π
tg x ≠ 1 ⇔ x ≠		+ π*k
	4

PW: Zadanie 2: brakuje powołania się na ciągłość funkcji |sinx|.

Janek191: 2) ok

Janek191: Poprawka do 1)

	π
Dodatkowo x ≠		+ kπ
	2

Michał: @jacek191 Ok dzięki Janek =) jest super. Nie wiem czemu nie wpadłem na to od razu, bardzo dziękuję i dzięki za potwierdzenie że drugi przykład jest ok. @PW No i PW stwierdzenie że trzeba się powołać na ciągłość funkcjj |sin x| nic mi nie mówi, co więcej nie mam pojęcia jak miałbym się na to powołać

PW:

	1		1
A skąd wiesz, że jeżeli fmin=		i fmax=		, to f przyjmuje wszystkie wartości
	3		2

	1		1
między		a		?
	3		2

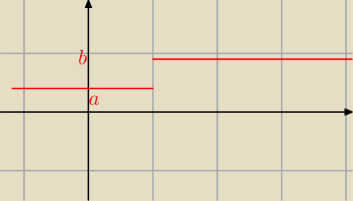
PW: Popatrz: funkcja osiąga minimum równe a oraz maksimum równe b. Nieprawda, że zbiorem wartości jest przedział <a, b>.

Michał: No wynika to chyba z tego że f(D) |sinusa| = <0;1> i większy wartości sin nie przyjmie w takiej postaci czyli podstawiajac do wzoru jego max i minimalna wartość otrzymam wartośc max i min funkcji, bo funkcja składa się oprócz |sin| z stałych. Nie wiem, czy to brzmi przekonująco, ale tak mi się wydaje to działa ;_;

Michał: Ok... Co do rysunku, to co zatem będzie tym przedziałem, skoro <a;b> nim nie jest?

PW: Źle to tłumaczysz, a sprawa jest ważna − widzisz jaki prosty kontrprzykład można wymyślić. Wystarczyło napisać: ponieważ funkcja |sinx| jest ciągła, przyjmuje wszystkie wartości między 0 a 1, wobec czego f(x) przyjmuje wszystkie wartości między

	1		1
		a		.
	2+1		2+0

PW: Na pytanie z 19:30. Zbiorem wartości jest dwupunktowy zbiór {a, b}, to nie przedział <a, b>.

Michał: Ah rozumiem już o co się rozchodzi.Dobra,masakra Dziękuję PW za rozwinięcie, to takie trochę podświadome mi się wydaje, ale pewnie masz rację, że należy to napisać. Dzięuję za mądrą radę, postaram się do niej stosować. CO prawda słabo formuluje wnioski, no ale prkatyka czyni mistrza, moze kiedyś się nauczę!