plani pppk: Punkkt S jest środkiem okręgu opisanego na trójkącie ostrokątnym ABC. Udowodnij, że suma miar kątów ABS i ACD równa się 90.

ite:

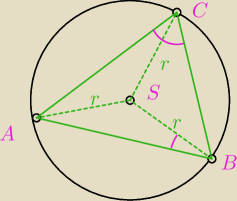
	1
|<ACB|=		|<ASB| // kąty wpisany i środkowy oparte na tym samym łuku
	2

ΔASB równoramienny więc |<ABS|=|<SAB| w ΔASB |<ASB|=180^o−|<ABS|−|<SAB|=180^o−2|<ABS|

	1		1
|<ACB+|<ABS|=		|<ASB|+|<ABS|=		(180o−2|<ABS|)+|<ABS|=
	2		2

=90^o−|<ABS|+|<ABS|=90^o

pppk: dzięki