| 1 | ||
f(x) = | x3 + 2x2−3x | |
| 3 |

 http://www.wolframalpha.com/input/?i=x%5E3%2F3%2B2x%5E2-3x
http://www.wolframalpha.com/input/?i=x%5E3%2F3%2B2x%5E2-3x
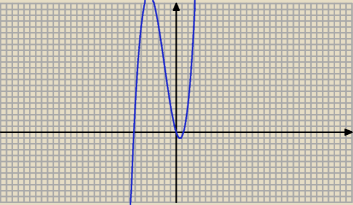 f '(x) = x2 + 4 x − 3 = 0
Δ = 16 − 4*1*(−3) = 28 = 4*7 √Δ = 2√7
f '(x) = x2 + 4 x − 3 = 0
Δ = 16 − 4*1*(−3) = 28 = 4*7 √Δ = 2√7
| − 4 − 2√7 | − 4 + 2√7 | |||
x1 = | = − 2 − √7 x2 = | = − 2 + √7 | ||
| 2 | 2 |