pomocy imie: wyznacz równanie asymptoty

	x3
f(x) =
	x2+x−2

ekstrema i przedziały monotoniczności

	x2
f(x)=
	3x−1

pole obszaru ograniczonego y=x², y=−x²+2x prosze o rozwiazanie jednego chociaz zadanka dziekuje

imie: pomocy chociaz pierwsze

xyz: Nie pros o rozwiazanie tylko o zrozumienie jak sie to liczy 1. sprawdzamy czy jest asymptota pionowa, czyli szukamy miejsc zerowych mianownika x²+x−2 = 0 Δ = 1 + 8

	−1−3
x1 =		= − 2
	2

	−1+3
x2 =		= 1
	2

i liczymy granice lewo i prawo stronne w x=−2 i w x=1 (juz moglbym stwierdzic ze sa, ale formalnie to):

	x3		−8
lim		=		= − ∞
	(x+2)(x−1)		0+

x−>−2⁻

	x3		−8
lim		=		= ∞
	(x+2)(x−1)		0−

x−>−2⁺ zatem x = − 2 to asymptota pionowa obustronna(bo raz jest −∞, a raz jest ∞) jakby byla tylko −∞ to wtedy jest pionowa lewostronna itd.

	x3		1
lim		=		= − ∞
	(x+2)(x−1)		0−

x−>1⁻

	x3		1
lim		=		= ∞
	(x+2)(x−1)		0+

x−>1⁺ zatem x = 1 to asymptota pionowa obustronna. asymptoty poziome to badanie granicy w −∞ oraz ∞ zatem

	x3
lim		= − ∞
	(x+2)(x−1)

x−>−∞

	x3
lim		= ∞
	(x+2)(x−1)

x−>∞ tutaj granice wyszly nieskonczonosc wiec nie ma asymptoty poziomej (jakby wyszla konkretna liczba np. −4, 0 czy 55 to by asymptota istniala)

jc:

x3		3x−2
	=x−1 +
x2+x−2		x2+x−2

Wniosek. Asymptoty w +∞ i w −∞: y=x−1.

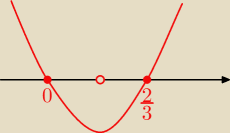
xyz: zad 2. Ekstrema i przedziały monotoniczności:

	x2
f(x) =
	3x−1

	1
założenia co do dziedziny: x ≠
	3

	2x*(3x−1) − (3)*(x2)		6x2−2x−3x2		3x2−2x
f '(x) =		=		=
	(3x−1)2		(3x−1)2		(3x−1)2

sprawdzamy ekstrema: f '(x) = 0

3x2−2x
	= 0
(3x−1)2

3x² − 2x = 0 x(3x−2) = 0

	2
x = 0 lub 3x=2 −−> x =
	3

dla x ∊ (−∞;0) f '(x) > 0 funkcja rosnie

	1		1		2
dla x ∊ (0;		) U (		;		) f '(x) < 0 funkcja maleje
	3		3		3

	2
dla x ∊ (		;∞) f '(x) > 0 funkcja rosnie
	3

	0
dla x = 0 mamy ekstremum lokalne maksimum, a jego wartosc: f(0)=		=0
	0−1

	2
dla x =		mamy ekstremum lokalne minimum,a jego wartosc:
	3

	2		2   ( )2   3		4   9		4
f(		) =		=		=
	3		2   3* −1   3		1		9

imie: dziękuje dobry czlowieku

jc:

	x2		1		1		4
f(x)=		=		[(3x−1) +		+2] ≥
	3x−1		9		3x−1		9

Równość zachodzi w przypadku 3x−1=1, czyli dla x=2/3.

jc: Tak jest dla x>1/3. Zapomnij o tym, co napisałem.

imie: ok thx