zad adam: 7. Jeden z boków trójkąta leży na płaszczyźnie Π. Pozostałe boki tworzą z płaszczyzną Π kąty α i β, a rzuty prostopadłe tych boków na tę płaszczyznę są do siebie prostopadłe. Znaleźć tangens kąta nachylenia płaszczyzny trójkąta do płaszczyzny Π. Przyjmując, że bok trójkąta leżący na płaszczyźnie Π ma długość a, wyznaczyć odległość punktu przecięcia rzutów pozostałych boków na płaszczyznę Π od płaszczyzny trójkąta.

Mila: Licz.

adam: jak?

Mila: Jeśli masz odpowiedź to napisz. Liczę.

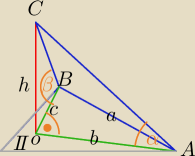
Mila: |OC|=h, OC⊥π

	h
1) w Δ COB: tgβ=		⇔h=c*tgβ
	c

	h
2) W ΔCOA: tgα=		⇔h=b*tgα
	b

z (1) i (2) c*tgβ=b*tgα

	b*tgα
c=
	tgβ

3) W ΔAOB: a²=c²+b²

	b2*tg2α
a2=		+b2
	tg2β

	tg2α		tg2α+tg2β
a2=b2*(		+1)⇔a2=b2*		⇔
	tg2β		tg2β

	a2*tg2β
b2=
	tg2α+tg2β

	a*tgβ		a*tgα
b=		i c=
	√tg2α+tg2β		√tg2α+tg2β

4) Obliczamy wysokość w ΔAOB opuszczoną na AB (porównanie pola b*c=a*h_p)

	a*tgα*tgβ
hp=
	tg2α+tg2β

5) Odległość punktu o od ściany ABC. Policzysz ?

adam: postaram się

Mila: A odpowiedź masz?

adam: nie mam

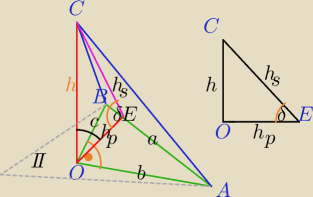
Mila: OC⊥OE, OE⊥AB

	h
5) tgδ=
	hp

	tg2α+tg2β
tgδ=c*tgβ*		=
	a*tgα*tgβ

	a*tgα		tg2α+tg2β
=		*		⇔
	√tg2α+tg2β		a*tgα

tgδ=√tg²α+tg²β −tangens kąta nachylenia płaszczyzny trójkąta do płaszczyzny Π. =====================

Mila: Obliczyłeś tę odległość ?

adam: A jak ją obliczyć?

Mila: To będzie wysokość ΔCOE opuszczona z wierzchołka O na bok CE. Kombinuj, przecież nie mogę wszystkiego za Ciebie liczyć. Skąd masz to zadanie? Jest ciekawe.

adam: A to wtedy też z równości pól można wyliczyć

adam:

h
	=sinδ
hs

	h
hs=
	sinδ

z pól:

h
	*x=h*hp
sinδ

	h*hp*sinδ
x=		=hpsinδ
	h

adam: Mila, pomóż mi

Mila: To jest dobrze, ale trzeba wyznaczyć sinδ, sporo przekształceń tą drogą.

	sin2δ
tg2δ=
	cos2δ

	sin2δ
tg2α+tg2β=
	1−sin2δ

tg²α+tg²β=u u*(1−sin²δ)=sin²δ u=sin²δ+u*sin²δ u=sin²δ*(1+u)

	u
sin2δ=
	1+u

	√tg2α+tg2β
sinδ=
	1+√tg2α+tg2β

Posprawdzaj rachunki. Jutro pomyślę jeszcze i przeliczę na konkretach.

Mila: Pierwiastek w mianowniku popraw.