 Witam, prosiłbym o pomoc z zadaniem z mechaniki.
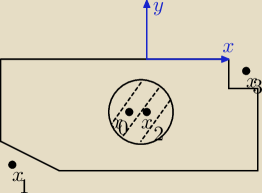
Należy obliczyć środek ciężkości przedstawionej figury (z widocznym wyciętym trójkątem, kołem i
kwadratem).
Punkty (x1,y1), (x2,y2), (x3,y3) to środki ciężkości wyciętych figur, analogicznie dla tych
figur zdefiniowane są ich pola obszarów P1, P2, P3.
W obliczeniach należy wykorzystać obszar całego prostokąta P0 (w którego skład wchodzi cała
figura), ze środkiem ciężkości w punkcie (x0, y0) i odpowiednio 'odjąć' od niego wycinki.
Nie wiem jednak, jak dokładnie wyglądać powinien wzór na współrzędną środka ciężkości tej
figury, z racji, że układ współrzędnych jest w takim miejscu i czy we wzorze nie należy
dodatkowo zmienić gdzieś znaków na przeciwne. Zastanawiam się też, jak wyglądałby on, gdyby
figura zaczynała się w początku układu współrzędnych.
Z góry dziękuję za pomoc ze znalezieniem tych wzorów.
Pozdrawiam.
Witam, prosiłbym o pomoc z zadaniem z mechaniki.
Należy obliczyć środek ciężkości przedstawionej figury (z widocznym wyciętym trójkątem, kołem i
kwadratem).
Punkty (x1,y1), (x2,y2), (x3,y3) to środki ciężkości wyciętych figur, analogicznie dla tych
figur zdefiniowane są ich pola obszarów P1, P2, P3.
W obliczeniach należy wykorzystać obszar całego prostokąta P0 (w którego skład wchodzi cała
figura), ze środkiem ciężkości w punkcie (x0, y0) i odpowiednio 'odjąć' od niego wycinki.
Nie wiem jednak, jak dokładnie wyglądać powinien wzór na współrzędną środka ciężkości tej
figury, z racji, że układ współrzędnych jest w takim miejscu i czy we wzorze nie należy
dodatkowo zmienić gdzieś znaków na przeciwne. Zastanawiam się też, jak wyglądałby on, gdyby
figura zaczynała się w początku układu współrzędnych.
Z góry dziękuję za pomoc ze znalezieniem tych wzorów.
Pozdrawiam.
| Sy | Sx | |||
xc= | oraz yc= | gdzie: | ||
| P | P |
 W przypadku trójkąta P1, obie współrzędne będą na minusie. W kwadracie P3 obie natomiast są
dodatnie. Koło P2 ma prawdopodobnie pierwszą współrzędną równą zero, a drugą ujemną.
Gdyby figura znajdowała się w początku układu współrzędnych, środki figur prostych miałaby inne
współrzędne, xc oraz yc dostałbys inne − ale koniec końców środek trafiłby w to samo
miejsce
W przypadku trójkąta P1, obie współrzędne będą na minusie. W kwadracie P3 obie natomiast są
dodatnie. Koło P2 ma prawdopodobnie pierwszą współrzędną równą zero, a drugą ujemną.
Gdyby figura znajdowała się w początku układu współrzędnych, środki figur prostych miałaby inne
współrzędne, xc oraz yc dostałbys inne − ale koniec końców środek trafiłby w to samo
miejsce
