Przekątna trapezu zawiera się w dwusiecznej, oblicz pole i długość boków. Łukasz: Miara kąta ADC trapezu ABCD jest równa 120⁰, a przekątna BD jest zawarta w dwusiecznej tego kąta. Przekątne trapezu przecinają się w punkcie E takim, że |AE|=14 i |EC|=7. Oblicz długości boków i pole trapezu, jeśli AB || CD.

Blee: Bzdura ... przekatna BD nie moze byc dwusieczna kata ADC. Gdyby tak bylo to kat DBC = 0

Blee: Wroc ... przyjalem (nie wiedziec czemu) ze to jest trapez rownoramienny

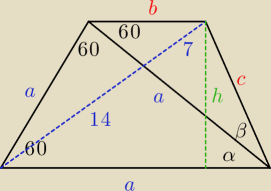
Blee: 1) α = 180 − 60 − 60 = 60 2) czyli |AB| = |BD| = |AD| = a

	a		14
3) z podobieństwa trójkątów wynika, że:		=		−> a = 2b
	b		7

	a√3
4) h =		(wysokość trapezu = wysokość Δrównobocznego)
	2

czyli mamy:

	a		a√3
(		)2 + (		)2 = (14+7)2
	2		2

a2 + 3a2
	= 212
4

a² = 21² −> a = 21

	21
czyli b =
	2

i teraz np. z tw. cosinusów wyznaczasz 'c' c² = a² + b² − 2ab*cos60^o

Łukasz: Dzięki wielkie za odpowiedź. Do którego trójkąta został użyty pitagorasz (chyba) w podpuncie 4?

marcinek: na jakiej zasadzie przyjmujesz że kąt DAB ma również 60°?

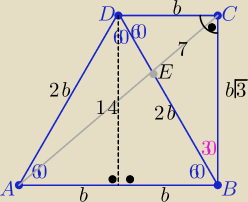
Eta: Taki trapez składa się z trzech trójkątów "ekierek" o katach 30^o,60^o, 90^o

	AB
i jest trapezem prostokątnym ( bo		=14/7 ⇒ |AB|=2b
	DC

Z tw. Pitagorasa w ΔABC (2b)²+(b√3)²=21² ⇒ 7b²=21*21 ⇒ b²=63 ⇒ b=3√7 to |AB|=2b=6√7, |DC|=b=3√7 , |AD|=2b=6√7, |BC|=b√3=3√21 =============================================

	1
P= 3*P(ΔDCB)= 3*		*b*b√3
	2

	3*63√3		189√3
P=		=
	2		2

===================

Eta: kąty ABD i BDC −−− naprzemianległe więc trójkąt ABD równoboczny