objętość ostrosłupa mat: Oblicz objętość ostrosłupa prawidłowego czworokątnego wiedząc że odległości środka wysokości ostrosłupa od ściany bocznej i od krawędzi bocznej są odpowiednio równe n i m

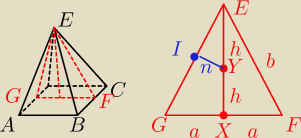
Blee: Część I mamy podobieństwo trójkątów: ΔEXG ∼ ΔEIY więc:

b		a
	=
h		n

z tw. Pitagorasa wiemy także, że: a² + 4h² = b²

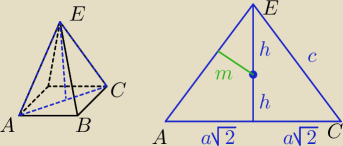
Blee: Część II Analogiczne podobieństwo trójkątów, z czego mamy:

c		a√2
	=
h		m

dodatkowo z tw. Pitagorasa: 2a² + 4h² = c² DODATKOWO: patrząc na ścianę boczną, wiemy że: (|FE|)² + (|CF|)² = (|CF|)² ⇔ b² + a² = c² W sumie masz 5 równań z 5'cioma niewiadomymi (a,b,h oraz n,m). Wyznaczasz a,h za pomocą n,m i wyznaczasz objętość tegoż ostrosłupa. Powodzenia

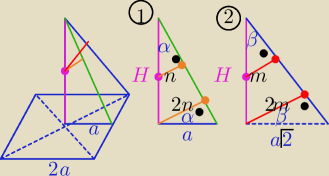
Eta: Łatwiej jest tak: ( bez 5−iu równań

	1		4
V=		4a2*H =		a2*H
	3		3

Należy wyrazić a i H za pomocą n i m

	2n		2n		2m		2m
z 1/ sinα=		i cosα=		z 2/ sinβ=		i cosβ=
	H		a		H		a√2

z jedynki trygonometrycznej

4n2		4n2		4m2		2m2
	+		=1 i		+		=1
H2		a2		H2		a2

i mamy układ równań z dwoma niewiadomymi "a" i "H" Rozwiązując ten układ równań ...... otrzymasz:

	4n2m2		2nm
H2=		⇒ H=
	2n2−m2		√2n2−m2

	2n2m2
i a2=
	m2−n2

to V=..................

	16m3n3
V=
	3(m2−n2)(√2n2−m2

===================== Sprawdź rachunki.... lub sprawdź zgodność z odpowiedzią ...