wykaż że, równoległobok Natt: Dany jest równoległobok ABCD w którym |AB| > ||BC| i kąt BAD jest ostry, Wykaż, że dwusieczna kąta BAD dzieli bok CD na dwa odcinki, takie,że długośc jednego z nich jest równa |CD| − |BC|. Ktoś ma jakiś pomysł jak to rozwiązać?

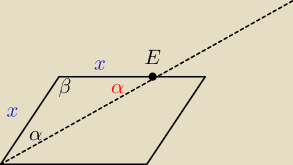
Blee: 1) zauważamy, że ∡DEA = ∡EAB = α 2) stąd wiemy, że ΔAED jest równoramienny 3) wiemy, że |AD| = |DE| 4) w takim razie |CE| = |CD| − |DE| = |CD| − |AD| = |CD| − |BC| c.n.w.