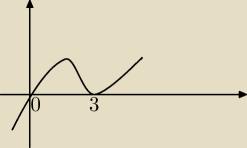
Wskaż przedział, w którym wielomian f(x)= x^3-6x^2+9x jest funkcją malejącą. mak: Wskaż przedział, w którym wielomian f(x)= x³−6x²+9x jest funkcją malejącą. A. <1,3> B. <0,4> C. (−∞, 0) D. (−3,−1) f(x)= x³−6x²+9x=x(x²−6x+9)=x(x−3)² Funkcja malejąca jest w przedziale <1,3> (taka jest odpowiedź). Skąd wiadomo, że maleje od 1?

Blee: Rysunek masz w zadaniu podany? Na dobrą sprawę nie wiesz tego, ale jest to jedyna możliwa odpowiedź, a jest to pytanie testowe, więc nie powinieneś się tym jakoś bardzo martwić (tak wiem − trochę to głupie).

Janek191: f '(x) = 3 x² − 12 x + 9 = 3*( x² − 4 x + 3) = 3*( x − 1)*(x −3) < 0 dla x ∊( 1 , 3) więc wielomian maleje w ( 1, 3).

mak: Rysunek nie był podany w zadaniu. Dzięki za odpowiedzi, rozumiem już