Równanie |(x+2)^2-3|=2a+1 z niewiadomą x ma dokładnie trzy rozwiązania mak: Równanie |(x+2)²−3|=2a+1 z niewiadomą x ma dokładnie trzy rozwiązania tylko wtedy, gdy: A. a=−2 B. a=0 C. a=1 D. a=3

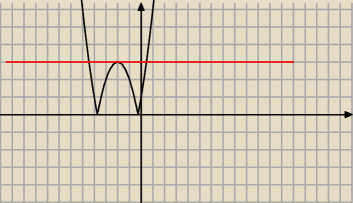
Krzysiek60: c) a=1

kl:

Mila: 1) |(x+2)²−3|=2a+1 f(x)=(x+2)²−3 parabola skierowana ramionami do góry W(−2,−3) wsp. wierzchołka paraboli ( W leży poniżej osi OX) W'(−2,3) wsp. punktu symetrycznego do W względem OX . 2a+1=3 2a=2 a=1 Prosta y=3 przetnie wykres |f(x)| w trzech punktach.

Tang Xin: Czyli dobrze napisałem wtedy

Mila: Oczywiście, że dobrze, chciałam pokazać sposób bez rysowania wykresu, korzystając z własności funkcji kwadratowej.