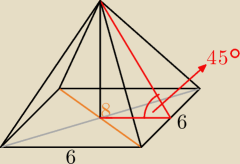
Podstawą ostrosłupa jest romb. Oblicz V i Pc. mak: Podstawą ostrosłupa jest romb, w którym krawędź podstawy jest równa 6 i krótsza przekątna 8. Ściany boczne ostrosłupa są nachylone do podstawy pod kątem 45°. Oblicz objętość i pole powierzchni całkowitej tego ostrosłupa. Z tw. πtagorasa wyliczyłem długość dłuższej przekątnej = 4√5. Następnie pole rombu:

8+4√5
	=4+2√5 Podstawiłem to do pola rombu = ah, gdzie a=6:
2

	4+2√5		2+√5
4+2√5=6h ⇒ h=		=
	6		3

	2+√5
Ten czerwony mały odcinek to połowa wysokości rombu, więc równa się		A druga kreska
	6

	2+√5		2√2+√10
czerwona pochylona to przekątna kwadratu, więc:		*√2 =
	6		6

	1		2+√5		4√5
V=		*(4+2√5)*		=		+1
	3		6		9

Pc=4+2√5+4*(6*U{2√2+√10{6})=2(2+4√2+√5+2√10) Czy to jest dobrze zrobione? Biorąc pod uwagę te dziwne wyniki, mogłem gdzieś popełnić jakiś błąd. Na forum było już takie zadanie, ale niewiele zrozumiałem z tamtego tłumaczenia, a i pole rombu wyszło mi inne. Byłbym wdzięczny za wzgląd w moje rozwiązanie.

mak: Aaah, tyle pisania, a dopiero teraz zauważyłem błąd. W polu rombu dodałem dwie przekątne, a nie pomnożyłem ich. Jak rozwiążę dalej tak jak rozwiązałem, tylko że z dobrym już wynikiem pola rombu, to będzie dobrze, prawda?

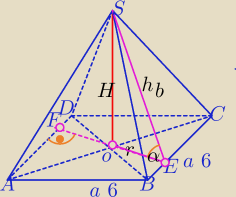Mila: Błędnie zaznaczyłeś kąt, to jest kąt dwuścienny. Tak byłoby, gdyby w podstawie był kwadrat. Przecinamy ostrosłup płaszczyzną prostopadłą do BC i przechodzącą przez wysokość OS. |DB|=8, α=45^o⇒H=|OE|=r |EF|=h=2r a=6 1) |AC|=4√5

	8*4√5
P▱=		=16√5
	2

a*h=16√5⇔6*h=16√5

	8√5
2) h=
	3

	4√5
r=		=H
	3

3)

	4√5		4√10
hb=		*√2=
	3		3

	1		4√5		320
4) V=		*16√5*		=
	3		3		9

	4√10
Pc=16√5+4*6*
	3