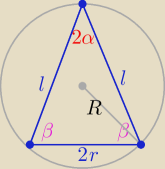
Stożek wpisany w kule Kalirr: Stosunek pola powierzchni bocznej stożka do pola powierzchni kuli opisanej na tym stożku wynosi 3:8. Wyznacz miarę kąta rozwarcia tego stożka. Witam. Zrobiłem to zadanie pewnym sposobem ale wyszedł zły wynik. Gdzie jest błąd? α− połowa kąta rozwarcia β− kąt przy podstawie R− promień kuli

πrl		3
	=
4πR2		8

12R²=8rl

r		l
	=
sinα		sinβ

sinβ=sin(90−α)=cosα r=2Rsinα l=2Rcosα 12R² = 16R²(2sinαcosα)

	3
sin2α=
	4

Mila: Jaka jest odpowiedź, liczę.

Eta: Z treści zadania:

rl		3		r		l		3
	=		/:2 ⇒		*		=
R2		2		R		2R		4

Z tw. sinusów

r		l
	=sin(2α) i		=cosα
R		2R

zatem: 4sin(2α)*cosα=3 ⇒8sinα(1−sin²α)−3=0 8sin³α−8sinα−3=0 i W(1/2) =1−4+3=0 to sinα=1/2 ⇒ α=30^o to 2α= 60^o ======== wtedy przekrojem jest trójkąt równoboczny o boku 2r lub ( dzieląc Hornerem otrzymujemy drugie równanie : 4sin²α+2sinα−3=0 i α∊(0^o,90^o) bo 2α∊(0,180^o)

	√13−1
sinα=		≈ 0,6514
	4

to α≈ 40,5^o więc 2α≈ 81^o =======

Mila:

	πrl		3		r*l		3
1)		=		⇔		=
	4πR2		8		R2		2

	2r
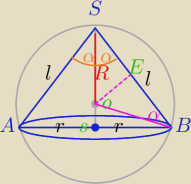
2)		=2R z tw. sinusów w ΔABC
	sin(2α)

r
	=sin(2α)
R

	r		l		3
3) Z(1)		*		=
	R		R		2

	0.5l
W ΔSEO: cosα=
	R

	l		3
sin(2α)*		*2=
	2R		2

	3
sin(2α)*cosα=
	4

	3
2 sinα*cos2α=
	4

	3
2*sinα*(1−sin2α)=
	4

	3
2sinα−2sin3α−		=0⇔
	4

8sin³α−8sinα+3=0 i sinα>0

	1		1		√13		1		√13
sinα=		lub sinα=−		+		lub sinα=−		−		∉D
	2		4		4		4		4

	π		π
α=		to 2α=		lub sinα≈0.65138⇔α≈40.5⇔2α≈81o
	6		3

===============================

Eta: Nawet przybliżenia nam się zgadzają

Mila: A Kalirrrr śpi.

Eta: