Prosze o rysunek👏 Pilne👏: w graniastoslupie prawidlowym czworokatnym o krawedzi podstawy a przekatna graniastoslupa tworzy ze sciana boczna kat alfa. oblcz objetosc i pole powierzchni calkowitej graniastoslupa. Dla jakich alfa zadanie ma tozwiazanie?

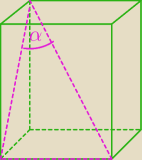
iteRacj@: na rysunku jest zaznaczony α kąt pomiędzy przekątną graniastoslupa a ścianą boczną

Help me: Dzieki a umie ktos to rozwiazac?

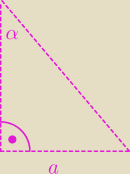
iteRacj@: Ty umiesz rozwiązać, powstał łatwy trójkąt prostokatny. Skorzystaj z funkcji trygonomtrycznych kąta α, dasz radę.

Burak: Próbowałam ale na takich liczbach mi nie wychodzi np sinα= a/ przeciwprostokatna i co dalej mam zrobic ?

iteRacj@:

	a
skoro, tak jak piszesz sin α=
	przeciwprostokatna

	a
to przeciwprostokątna=		i masz obliczoną długość przekątnej graniastosłupa
	sin α

Burak: No w sumie tak ale zeby obliczyc objetosc i Pc to musze miec H i probowalam z Tw pitagorasa ze przekatna podstawy to a √2² +H²= a/sinα ² ale nie wiem czy to tak ? Bo takie jakies dziwne liczby wychodza ze nie wiem co dalej

iteRacj@: bardziej przyda Ci się wyliczenie przekątnej ściany bocznej z tangensa kąta α, potem z tw. Pitagorasa oblicz krawędź ściany bocznej i zostanie tylko podstawienie do wzoru na objętość prostopadłościanu

iteRacj@: masz błąd w równości 18:47 powinno być

	a
(√2*a)2 +H2= (		)2
	sin α

z tego też możesz wyliczyć H

Burak: Wyszlo mi ze tgα=a/przekatna sciany bocznej ...z tego obliczylam przekatna =tgα/a ale jak wstawiam do tw pitagorasa mam a²+(tgα/a )²=H² dobrze ? bo i tak utknelam na tym

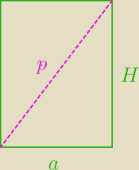
iteRacj@: błąd w zastosowaniu tw. Pitagorasa p − przekątna ściany bocznej p²=a²+H²

	a
poza tym p=		− spójrz poprzedni rysunek z 18:21
	tg α

iteRacj@: 18:54 tg α prawidłowo, ale źle wyliczyłaś z tego p