Help Pomocys: W graniastoslupie prawidlowym trojkatnym pole powierzchni bocznej jest rowne sumie pol obu podstaw. Oblicz sinus kata nachylenia przekatnej sciany bocznej do sasiedniej sciany bocznej

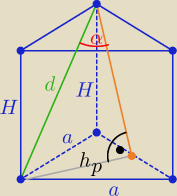
Eta: 1/ rysunek 2/ z treści zadania 2P_p=P_b

	a2√3
2*		=3aH
	4

a√3=6H ⇒ a= 2H√3

	a√3
hp=		= .....=3H
	2

d=√H²+a²= √H²+12H²= H√13 to

	hp		3H
sinα=		=
	d		H√13

sinα=3√13/13 ============

Basia:

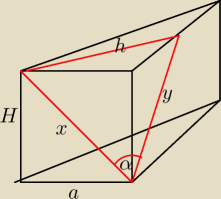
	a2√3		a2√3
3a*H = 2*		=		/:3a
	4		2

	a√3
H =
	6

	a√3
h =
	2

	a2*3		39a2
x2 = H2+a2 =		+a2 =
	36		36

	a√39
x =
	6

	a		3a2		a2		12a2
y2 = H2+(		)2 =		+		=
	2		36		4		36

	a√12
y =
	6

h² = x²+y²−2xy*cos α

3a2		39a2		12a2		a√39		a√12
	=		+		− 2*		*		*cos α /*36 /:a2
4		36		36		6		6

27 = 39 + 12 − 2√39*√12cos α 2*√3*13*√3*4cos α = 24 2*3*2*√13*cos α =24

	2
cosα =
	√13

	3		3√13
sinα = √1−(4/13) = √9/13 =		=
	√13		13

mogłam się gdzieś pomylić

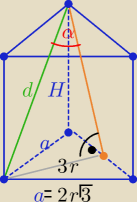Eta: 2 sposób h_p=3r , r −−− dł . promienia okręgu wpisanego w podstawę to a= 2r√3 −−−− dł. krawędzi podstawy P_p = 3r²√3 z treści zadania 6r²√3= 6r√3*H ⇒ H=r d=√a²+H²= √12r²+r²= r√13

	3r
sinα=
	d

sinα= 3√13/13 =============

Pomocys: Dziekuje

Eta: