romb
maturka: Niech ABCD będzie rombem o kącie ostrym A równym 60 stopni; Punkty M i N znajdują się
odpowiednio po bokach AD i CD tak, że DM + DN = AB.
Wykazać, że trójkąt BMN jest równoboczny.
11 mar 12:52
maturka: Niech ABCD będzie rombem o kącie ostrym A równym 60 stopni; Punkty M i N znajdują się
odpowiednio na bokach AD i CD tak, że DM + DN = AB.
Wykazać, że trójkąt BMN jest równoboczny.
11 mar 13:20
maturka: up
11 mar 15:27
Eta:
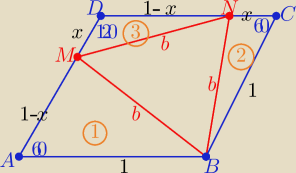
1/ rysunek
2/ przyjmujemy ( bez straty ogólności) romb o boku 1
to z treści zadania ⇒ |DM|=x i |DN|=1−x , x∊(0,1)
z twierdzenia cosinusów w każdym z trójkątów :
1) b
2=1
2+(1−x)
2−2*1(1−x)*cos60
o =.......... = x
2−x+1
2) b
2=1
2+x
2−2*1*x*cos60
o = ............... = x
2−x +1
3) b
2=x
2+(1−x)
2−2*x*(1−x)*cos120
o =..........= x
2−x+1
wniosek......... ΔBMN jest równoboczny
11 mar 15:39
maturka: dzieki
11 mar 15:44
Eta:

11 mar 15:47
 1/ rysunek
2/ przyjmujemy ( bez straty ogólności) romb o boku 1
to z treści zadania ⇒ |DM|=x i |DN|=1−x , x∊(0,1)
z twierdzenia cosinusów w każdym z trójkątów :
1) b2=12+(1−x)2−2*1(1−x)*cos60o =.......... = x2−x+1
2) b2=12+x2−2*1*x*cos60o = ............... = x2−x +1
3) b2=x2+(1−x)2−2*x*(1−x)*cos120o =..........= x2−x+1
wniosek......... ΔBMN jest równoboczny
1/ rysunek
2/ przyjmujemy ( bez straty ogólności) romb o boku 1
to z treści zadania ⇒ |DM|=x i |DN|=1−x , x∊(0,1)
z twierdzenia cosinusów w każdym z trójkątów :
1) b2=12+(1−x)2−2*1(1−x)*cos60o =.......... = x2−x+1
2) b2=12+x2−2*1*x*cos60o = ............... = x2−x +1
3) b2=x2+(1−x)2−2*x*(1−x)*cos120o =..........= x2−x+1
wniosek......... ΔBMN jest równoboczny
