trapez mat: W okrąg wpisano trapez o podstawach 13 i 5 i wysokości 3 Oblicz pole koła ograniczonego tym okręgiem

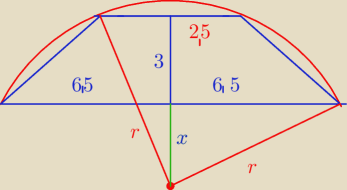
Janek191: I przypadek. Mamy r² = ( 3 + x)² + 2,5² r² = x² + 6,5² więc 9 + 6 x + x² + 6,25 = x² + 42,25 6 x = 42,25 − 9 − 6,25 6 x = 27 x = 4,5 r² = 4,5² + 6,5² = 20,25 + 42,25 = 62,5 P = π r² = 62,5 π ===============

Eta:

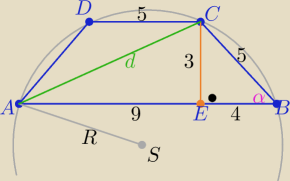
	3
w ΔEBC : |EB|=4 , |BC|=5 i d2=90 i sinα=
	5

z tw. sinusów w ΔABC

	d		d2		125
2R=		⇒ 4R2=		⇒ 4R2=250 ⇒ R2=		=62,5
	sinα		sin2α		2

P(koła)= 62,5π [j²] =============

Eta: O i mamy dwa sposoby A Janek bardzo "kocha" .......... ( oczywiście "x−sy"

Eta: A tam widzę wśród forumowiczów.... kogoś kto "kocha równoległoboki" Jak widać różne "miłości" ludzie mają

Kocham równoległoboki: to ja <3

Eta:

Krzysiek60: Dobrze A dlaczego ten trapez jest rownoramieny . ? czy przez to ze promien prostopadly do cieciwy dzieli ja na pol?

Eta: Każdy trapez wpisany w okrąg ............

Krzysiek60: Rownoramienny .