 1/ rysunek
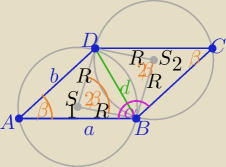
2/ z przystawania trójkątów ABC i BCD okręgi mają równej długości promienie R
oraz ΔBSD i BS2D też są przystające z cechy (bkb)
i kąty BAD i BS1D −− wpisany i środkowy oparty na tym samym łuku
zatem |<BS1D|= 2β
1/ rysunek
2/ z przystawania trójkątów ABC i BCD okręgi mają równej długości promienie R
oraz ΔBSD i BS2D też są przystające z cechy (bkb)
i kąty BAD i BS1D −− wpisany i środkowy oparty na tym samym łuku
zatem |<BS1D|= 2β
| 1 | ||
to P(BS1DS2) = 0,5 P(BS1D) P(BS1D)= | *R2*sin2β | |
| 2 |
| a2+b2+2abcosα | ||
4R2sin2α= a2+b2+2abcosα ⇒R2= | ||
| 4sin2α |
| a2+b2+2abcosα | ||
to P(BS1DS2)= − | *sin(2α) , sin(2α)=2sinα*cosα | |
| 4sin2α |
| a2+b2+2abcosα | ||
P= − | ||
| 2tgα |

