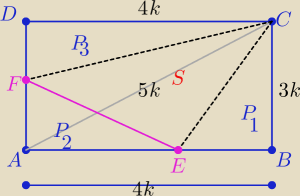
 Jeden ze sposobów
1/ rysunek zgodny z treścią zadania
2/ |AC|=5k ( z tw. Pitagorasa
3/ z tw. o dwusiecznej
Jeden ze sposobów
1/ rysunek zgodny z treścią zadania
2/ |AC|=5k ( z tw. Pitagorasa
3/ z tw. o dwusiecznej
| 3 | 3 | 5 | 5 | |||||
|EB|= | *|AB|= | k to |AE|= | *|AB|= | k | ||||
| 8 | 2 | 8 | 2 |
| 4 | 4 | 5 | 5 | |||||
|DF|= | *|AD|= | k to |AF|= | *|AD|= | k | ||||
| 9 | 3 | 9 | 3 |
| 1 | 3 | 9 | 27 | |||||
P1= | *3k* | k= | k2= | k2 | ||||
| 2 | 2 | 4 | 12 |
| 1 | 5 | 5 | 25 | |||||
P2= | * | k* | k= | k2 | ||||
| 2 | 2 | 3 | 12 |
| 1 | 4 | 32 | ||||
P3= | *4k* | k= | k2 | |||
| 2 | 3 | 12 |
| S | 5 | |||
to | = | |||
| P(ABCD) | 12 |
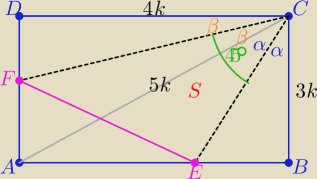 2 sposób
1/ i 2/ jak wyżej
3/ 2α+2β= 90o ⇒ α+β=45o=|<ECF|
4 z tw. o dwusiecznej
..........
Z tw. Pitagorasa w ΔDCF i BCE wyznacz długości |CF| i |CE|
2 sposób
1/ i 2/ jak wyżej
3/ 2α+2β= 90o ⇒ α+β=45o=|<ECF|
4 z tw. o dwusiecznej
..........
Z tw. Pitagorasa w ΔDCF i BCE wyznacz długości |CF| i |CE|
| 1 | ||
S= | *|CE|*|CF|*sin45o =........... | |
| 2 |
| S | 5 | ||
=...........= | |||
| P(ABCD) | 2 |
| S | 5 | ||
= ....= | |||
| P(ABCD) | 12 |