Okregi i odcinek
Blue Velwet : Dane sa okregi o(A,r) i o(B,r) oraz odcinek dlugosci d
Znajdz wszystkie punkty z ktorych kazdy jest oddalony od obu okregow o d
Ile jest takich punktow?
W odpowiedzi mam 0,1,2,3,4,5,6,7.,8,i nieskonczenie wiele
9 mar 20:39
Blue Velwet : Do tego zadania jak podejsc ?
Chociaz jeden z przypadkow ktos by pokazal .
9 mar 21:10
Janek191:
9 mar 21:19
Janek191:
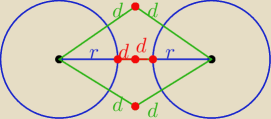
1) 1 punkt, gdy I A B I = 2 r +2 d
2) 2 punkty, gdy 2 r + 2 d > I A B I
9 mar 21:21
Blue Velwet : Janek 191 dziekuje CI ale niestety nic a nic z tego nie rozumiem
jesli mozesz inaczej to wytlumaczyc to prosze ale jesli nie to prosze sie nie klopotac
9 mar 21:30
iteRacj@:
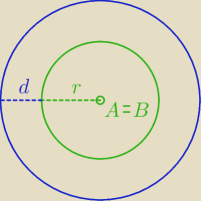
Może przypadek, gdy punktów oddalonych od obu okręgów o d jest nieskończenie wiele, będzie
prostszy do zrozumienia.
Jeśli punkty A i B pokrywają się, to
okręgi o(A,r) i o(B,r) też się pokrywają (mają takie
same promienie r). Wtedy punkty oddalone od nich o d tworzą
trzeci okrąg o środku w A=B
i promieniu
r+d. Punktów równooddalonych jest wtedy nieskończenie wiele.
9 mar 22:19
Blue Velwet: A jesliby r=d to wtedy punkty rownooddalone od A =B lezalaby na okregu zielonym ?
9 mar 22:28
iteRacj@:
nie, bo punkty mają byc równooddalone od okręgów a nie o środków A czy B
środek okręgu nie należy do okręgu
jeśli r=d to wtedy punkty równooddalone od obu okręgów leżą na okręgu o środku A=B i promieniu
r+d=2r
9 mar 22:36
Blue Velwet: iteRacj@ czy dobrze mysle ?
9 mar 22:36
Blue Velwet: Acha.
9 mar 22:37
iteRacj@:
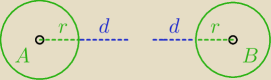
jeszcze przypadek gdy nie ma punktów równooddalonych od obu okręgów jest dość przejrzysty
czyli wtedy, gdy odległość pomiędzy środkami okręgów jest większa od 2r+2d
9 mar 22:44
Blue Velwet: Tak to widze i jest dla mnie zrozumiale .
9 mar 22:47
Blue Velwet:
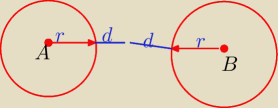
Jeszcze sobie wyobrazam taka sytuacje gdzie
AB= r+d+d+r= 2r+2d to bedzie jeden punkt rownooddalony od obu okregow
dalszse to proszse o pomoc
9 mar 22:53
iteRacj@:
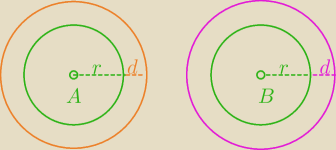
chyba najprościej będzie szukać tych punktów równooddalonych od obu okręgów o d tak:
wyobraź sobie (albo narysuj) wokół okręgu o(A,r) i wokół okręgu o(B,r) zbiór punktów odległych
o d
czyli okręgi i promieniach r+d i środkach odpowiednio A i B
potem
przesuwaj je, szukając punktów współnych
9 mar 22:58
iteRacj@:
ten jeden punkt znaleziony bardzo dobrze

9 mar 22:58
Blue Velwet: dziekuje za pomoc . Pozwolisz ze wrocimy do tego jutro .
Dobranoc
9 mar 22:59
iteRacj@:
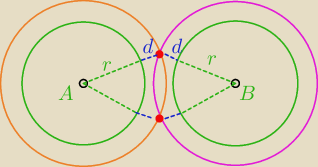
a to sytuacja, którą opisał
Janek191 o 21:19
9 mar 23:02
iteRacj@:
dobranoc
9 mar 23:03
iteRacj@:
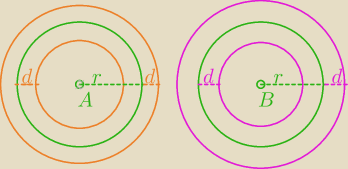
@
Blue Velwet
nie wiem, czy jutro będę na forum, więc teraz dorysuję do punktów równooddalonych z 22:58
(czyli okręgów i promieniach r+d i środkach odpowiednio A i B)
pozostałe punkty równooddalone czyli okręgi i promieniach r−d i środkach odpowiednio A i B
z tym kompletem można szukać pozostałych ilości punktów wspólnych
9 mar 23:37
iteRacj@:
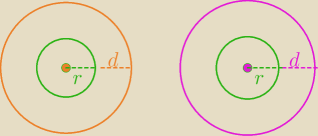
Ilość punktów wspólnych zależy od odleglości pomiędzy środkami o(A,r) i o(B,r) oraz od różnicy
długości promienia r i odcinka d.
Ta ostatnia różnica daje trzy przypadki:
1/ r−d<0 − rysunek z 22:58
2/ r−d>0 − rysunek z 23:37
3/ r−d=0 − rysunek powyżej w odległości d od środka okręgu leżą: punkty na okręgach o
promieniach r+d i
środki okręgów
10 mar 09:41

 Może przypadek, gdy punktów oddalonych od obu okręgów o d jest nieskończenie wiele, będzie
prostszy do zrozumienia.
Jeśli punkty A i B pokrywają się, to okręgi o(A,r) i o(B,r) też się pokrywają (mają takie
same promienie r). Wtedy punkty oddalone od nich o d tworzą trzeci okrąg o środku w A=B
i promieniu r+d. Punktów równooddalonych jest wtedy nieskończenie wiele.
Może przypadek, gdy punktów oddalonych od obu okręgów o d jest nieskończenie wiele, będzie
prostszy do zrozumienia.
Jeśli punkty A i B pokrywają się, to okręgi o(A,r) i o(B,r) też się pokrywają (mają takie
same promienie r). Wtedy punkty oddalone od nich o d tworzą trzeci okrąg o środku w A=B
i promieniu r+d. Punktów równooddalonych jest wtedy nieskończenie wiele.
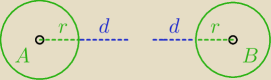 jeszcze przypadek gdy nie ma punktów równooddalonych od obu okręgów jest dość przejrzysty
czyli wtedy, gdy odległość pomiędzy środkami okręgów jest większa od 2r+2d
jeszcze przypadek gdy nie ma punktów równooddalonych od obu okręgów jest dość przejrzysty
czyli wtedy, gdy odległość pomiędzy środkami okręgów jest większa od 2r+2d
 Jeszcze sobie wyobrazam taka sytuacje gdzie
AB= r+d+d+r= 2r+2d to bedzie jeden punkt rownooddalony od obu okregow
dalszse to proszse o pomoc
Jeszcze sobie wyobrazam taka sytuacje gdzie
AB= r+d+d+r= 2r+2d to bedzie jeden punkt rownooddalony od obu okregow
dalszse to proszse o pomoc
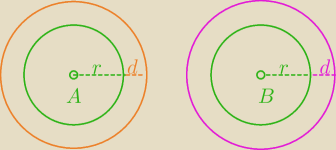 chyba najprościej będzie szukać tych punktów równooddalonych od obu okręgów o d tak:
wyobraź sobie (albo narysuj) wokół okręgu o(A,r) i wokół okręgu o(B,r) zbiór punktów odległych
o d
czyli okręgi i promieniach r+d i środkach odpowiednio A i B
potem przesuwaj je, szukając punktów współnych
chyba najprościej będzie szukać tych punktów równooddalonych od obu okręgów o d tak:
wyobraź sobie (albo narysuj) wokół okręgu o(A,r) i wokół okręgu o(B,r) zbiór punktów odległych
o d
czyli okręgi i promieniach r+d i środkach odpowiednio A i B
potem przesuwaj je, szukając punktów współnych

 a to sytuacja, którą opisał Janek191 o 21:19
a to sytuacja, którą opisał Janek191 o 21:19
 @Blue Velwet
nie wiem, czy jutro będę na forum, więc teraz dorysuję do punktów równooddalonych z 22:58
(czyli okręgów i promieniach r+d i środkach odpowiednio A i B)
pozostałe punkty równooddalone czyli okręgi i promieniach r−d i środkach odpowiednio A i B
z tym kompletem można szukać pozostałych ilości punktów wspólnych
@Blue Velwet
nie wiem, czy jutro będę na forum, więc teraz dorysuję do punktów równooddalonych z 22:58
(czyli okręgów i promieniach r+d i środkach odpowiednio A i B)
pozostałe punkty równooddalone czyli okręgi i promieniach r−d i środkach odpowiednio A i B
z tym kompletem można szukać pozostałych ilości punktów wspólnych
 Ilość punktów wspólnych zależy od odleglości pomiędzy środkami o(A,r) i o(B,r) oraz od różnicy
długości promienia r i odcinka d.
Ta ostatnia różnica daje trzy przypadki:
1/ r−d<0 − rysunek z 22:58
2/ r−d>0 − rysunek z 23:37
3/ r−d=0 − rysunek powyżej w odległości d od środka okręgu leżą: punkty na okręgach o
promieniach r+d i środki okręgów
Ilość punktów wspólnych zależy od odleglości pomiędzy środkami o(A,r) i o(B,r) oraz od różnicy
długości promienia r i odcinka d.
Ta ostatnia różnica daje trzy przypadki:
1/ r−d<0 − rysunek z 22:58
2/ r−d>0 − rysunek z 23:37
3/ r−d=0 − rysunek powyżej w odległości d od środka okręgu leżą: punkty na okręgach o
promieniach r+d i środki okręgów