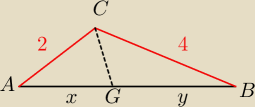
w trojkacie abc dan: W trojkacie ABC dlugosci bokow AC i BC sa odpowiednio rowne 2 i 4,zas miara kata ACB wynosi 120 stopni.Oblicz dlugosc odcinka ktory jest czescia wspolna dwusiecznej kata ACB i ABC. To zaczalem robic tak:

x		y
	=		<− twierdzenie o dwusiecznej
2		4

zatem y=2x. Potem twierdzenie cos 9x²=20−16*(−0,5)

	28
x2=
	9

	2√7
x=
	3

	4
wiec 3x=2√7 a wynik to		co robie zle?
	3

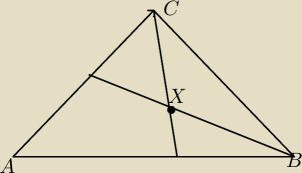
Blue Velwet : czescia wspolna dwusiecznej kąta ACB i dwusiecznej kąta ABC jest punkt X

Mila: Masz obliczyć długość |CG|. Dasz radę?

Mila: CG− odcinek dwusiecznej zawarty w ΔABC

dan: aaa to chodzilo o CG,tak dam rade,dziekuje

Blue Velwet : Mozna bylo napisac ze dwusiecznej kąta ACB i trojkata ABC

Mila: Dwusieczna to półprosta i nie można obliczyć jej długości, dlatego taka jest treść jak podano.

Eta:

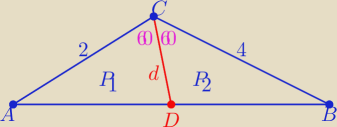
	1		4√3
P(ABC)=		*2*4*sin120o =
	2		2

	1		d√3		1		2d√3
P1=		*2*d*sin60o =		i P2=		*4*d*sin60o =
	2		2		2		2

to P₁+P₂=P ⇒ 3d√3=4√3 ⇒d=4/3