FUNKCJE bluee:

	1
Dana jest funkcja f określona wzorem f(x)=		−2. Uzasadnij, że najmniejszą liczbą
	x−1

całkowitą spełniającą nierówność f(8−x)≤f(2x) jest liczba 1.

	8
Liczyłam trzy raz, za każdym razem wychodzi x≤
	3

Jerzy: Z tego wynika,że źle liczysz. Pokaż te obliczenia.

bluee:

1		1
	−2≤		−2
8−x−1		2x−1

Taki mam start, jest OK

Jerzy: Tak.

Blee: Bluuee ... slowo klucz: CALKOWITA

Jerzy:

	1		1
Czyli masz:		≤
	7 − x		2x − 1

Blee: Oki ... teraz zauwazylem ze u Ciebie wychodzi niby x=2 jako rozwiazanie

bluee: Ja to −2 wciągnęłam do ułamków. Ty obustronnie dodajesz 2

bluee: Tak dokładnie mi wychodzi x=2 tyle, że NAJWIĘKSZA, a nie najmniejsza liczba całkowita spełniające równanie!

Jerzy: No pewnie, przecież to upraszcza rozwiązanie.

bluee: Punkt dla Ciebie, ja się męczyłam z tą 2 na całą A4.

bluee: Czy w takim razie mogę zrobić tak 2x−1≤7−x

bluee:

	1		1
Czy raczej		−		≤0 Dla pierwszej opcji znów wychodzi to samo.
	7−x		2x−1

Blee: Dla x∊(1/2 , 7) mamy 2x − 1 ≤ 7−x x≤8/3 No to sprawdzamy dla x=2 1/5 ≤ 1/3 i jest oki A co dla x>7 1−2x ≤ 7−x −6 ≤ x Czyli kazde x >7 Sprawdzenie, niech x = 100 1/(−93) ≤ 1/199 Zgadza sie. Czyli najwieksza wartosc nie istnieje.

bluee: Ale w zadaniu chodzi o najmniejszą wartość. I skąd wziąłeś te przedziały?

Blee: Achhh ... najmniejsza. To z pierwszego przedzialu mamy x=1 Drugi nas nie obchodzi Sprawdzamy co bedzie dla x<1/2 Wtedy mamy 2x−1 ≥ 7−x x ≥ 8/3 Czyli brak rozwiazan Wiec najmniejszym calkowitym bedzie x=1

Blee: Patrz kiedy zmienia sie znak mianownikow

bluee: W pierwszym przedziale nie ma najmniejszej wartości. I mógłbyś coś więcej o tych przedziałach ...

Blee: W pierwszym najmniejsze niema, ale jest najmniejsza CALKOWITA masz nierownosc jak mnozysz stronami przez cos to musisz rozpatrzyc dwie mozliwosci: 1) gdy jest to liczba dodatnia 2) gdy jest to liczba ujemna Tutaj beda w sumie 3 mozliwosc 1) pierwszy mianownik ujemny, drugi dodatni 2) dwa dodatnie 3) pierwszy dodatni, drugi ujemny Mnozac wtedy odpowiednio zmieniasz (lub nie) znak nierownosci

Jerzy:

	8
2x − 1 ≥ 7 − x ⇔ x ≥
	3

Wniosek: Najmniejszą liczbą całkowitą spełniającą tą nierówność jest liczba x = 3

Blee: Jerzy ... a dla jakich x masz taka postac tej nierownosci

bluee: Jak doszło do zmiany znaku .≤ na ≥

Jerzy: @Blee ... o jakich Ty przedziałach mówisz?

bluee: TEŻ CHCIAŁABYM WIEDZIEĆ.

Jerzy: OK.

	(2x − 1) − (7 −x)
Mamy nierówność:		≤ 0 ... i ją rozwiązujemy.
	(7 − x)(2x−1)

Jerzy: Czyli: (3x − 8)*(7 − x)*(2x − 1) ≤ 0

bluee: x∊¹₂∪⁸₃∪(8,∞)

bluee: Czyli najmniejsza liczba całkowita spełniająca równanie to x=1.

Blee: Jerzy a jak rozwiazujesz nierownosc: 1/x ≥ 2 Analogicznie tutaj czyli: 1) 7−x >0 i 2x−1 >0 2) 7−x < 0 i 2x−1 > 0 3) 7−x > 0 i 2x−1 < 0 4) 7−x < 0 i 2x−1 < 0 (to nigdy nie zachodzi)

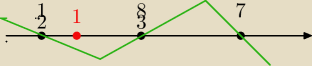
Jerzy: I widać,że najmniejszą liczbą całkowita spełniającą nierówność jest x = 1