Oblicz miarę kątów między przekątnymi Kar0lu: W czworokącie ABCD kąt BAC = 20°, kąt BCA ma miarę 35°, kąt BDC ma miarę 40°, kąt BDA ma miarę 70° . Na trójkącie ABC opisano okrąg. Znajdź miarę kąta między przekątnymi tego czworokąta. Prosiłbym o całkiem dokładne rozwiązanie i wyłumaczenie wszystkiego .

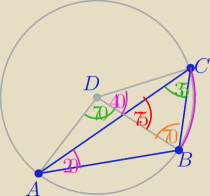
Eta: Warunki zadania są spełnione jeżeli Punkt D jest środkiem okręgu opisanego na trójkącie ABC ..................................... ................................ dokończ teraz już samodzielnie Odp: kąt ostry między przekątnymi 75^o lub kąt rozwarty między przekątnymi 105^o

Kar0lu: No tylko że nie wiem jak udowodnić że D jest środkiem tego okręgu

iteRacj@: z warunków zadania <BAC| = 20^o, |<BCA|=35^o, |<BDC|=40^o, |<BDA|=70^o w ΔDCB |<DCB|=180^o−40^o−70^o=70^o ⇒ ΔDCB równoramienny więc |DB|=|DC| |<CBA|=180^o−20^o−35^o=125^o |<DBA|=125^o−70^o=55^o w ΔDAB |<DAB|=180^o−55^o−70^o=55^o ⇒ ΔDAB równoramienny więc |DB|=|DA|

Kar0lu: "w ΔDCB |<DCB|=180o−40o−70o=70o ⇒ ΔDCB równoramienny" Skąd wzieło się to − 70 ° ? Bo raczej nie z treśdi zadania

iteRacj@: w ΔDCB |<DCB|=180^o−|<BDC|−|<CBD|=180^o−40^o−70^o=70^o

iteRacj@: które 70^o?

Eta: Przecież sam napisałeś to w treści !

Eta: Kąt BDA=70^o widnieje w treści

Kar0lu: Tylko że kąt BDA nie jest w tym trójkącie A kąd CBD nie jest dany w zadaniu Eta zaznaczyła go, ale to wynikało z tego że ona już miała założone że punkt D jest środkiem tego okręgu.