Dane są długości d1 i d2 Kasik: Przekątnych czworokąta wypukłego oraz jego pole P. Oblicz miare kąta przecięcia przekątnych jeśli: P=3 m², d1= √6 m d2 = √8m

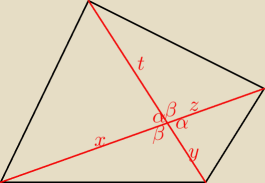
Basia: β=180−α z = √6−x t = √8−y

	1
P =		*[ xysin β + yzsin α + ztsin β + xtsin α]
	2

2P = x*y*sin(180−α)+y*(√6−x)*sinα + (√6−x)(√8−y)*sin(180−α) + x(√8−y)*sinα sin(180−α) = sinα 6 = sinα*[ xy + y√6 − xy + √48 − √6y − √8x + xy + x√8−xy ] 6 = √48*sin α

6

6

6

3

3√3

√3

sinα =

=

=

=

=

=

√48

√16*3

4√3

2√3

2*3

2

α = 60^o β = 120^o

Kasik: Dziękuje ale czy jest jakiś łatwiejsze rozwiązanie?

Basia: nie wiem

Eta:

	1
P=		d1*d2*sinα
	2

	1		√3
to		*√6*√8*sinα=3 ⇒ 2√3sinα=3 ⇒ sinα=
	2		2

to α=60^o lub α= 120^o

Eta: Pole czworokąta wypukłego jest równe połowie iloczynu długości przekątnych przez sinus kąta między tymi przekątnymi