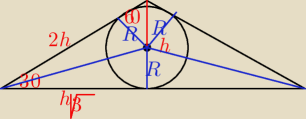
Odpowiedz to 4piS(7p{3}-12) Kasia: Wyznacz pole powierzchni kuli wpisanej w stozek, ktorego przekrojem osiowym jest trojkat rownoramienny o polu S i najwiekszym kacie rownym 120°

Basia:

	1		1
S = U{1}[2}*2h*R +		*2h*R +		*2h√3*R
	2		2

S = hR(1+1+√3) = hR(2+√3) S = h√3*h S = h²√3 h²√3 = hR(2+√3) h√3 = R(2+√3)

	h√3
R =
	2+√3

	h2*3		h2*√3*√3
P=4πR2 = 4π*		= 4π*		=
	(2+√3)2		4+4√3+3

	S√3		S√3(7−4√3)
4π*		= 4π*		=
	7+4√3		49−16*3

4π*S(7√3−12)

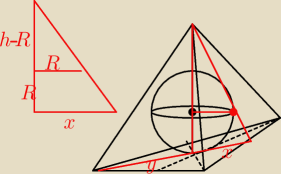
Kasia: Dziekuje bardzo, a wiesz moze jak rozwiazac: Krawedz podstawy ostroslupa prawidlowego trojkatnego ma dlugosc a, a krawędź boczna 2a. Wyznacz promien kuli wpisanej w ten ostoslup

Basia:

	1		a√3		a√3
x =		*		=
	3		2		6

	2		a√3		2a√3
y=		*		=
	3		2		6

y²+h²=(2a)²

4a2*3
	+h2 = 4a2
36

a2
	+h2 = 4a2
3

	12a2		a2		11
h2 =		−		=		{3}
	3		3		a2

	a√11
h =
	√3

z podobieństwa masz

R		h−R
	=
x		h

Rh = x(h−R) Rh = xh − xR Rh+Rx = xh R(x+h) = xh

	xh
R =
	x+h

podstaw wyliczone x i h, dokończ obliczenia

Kasia: Dziekuje Ci bardzo za pomoc